Rappels mathématiques
On connait la formule du théorème de Pythagore pour résoudre des problèmes sur les triangles.
[latex]a^{2}+b^{2}=c^{2}[/latex]
Face à la limitation engendrée par ce théorème, on a rapidement mis au point des tables qui associaient un angle du triangle rectangle à la longueur de ses côtés. Ces mesures ont été baptisées sinus pour le côté [latex]b[/latex], cosinus pour le côté [latex]a[/latex] et tangente pour le rapport entre les deux et représenté par l'angle [latex]\theta[/latex].
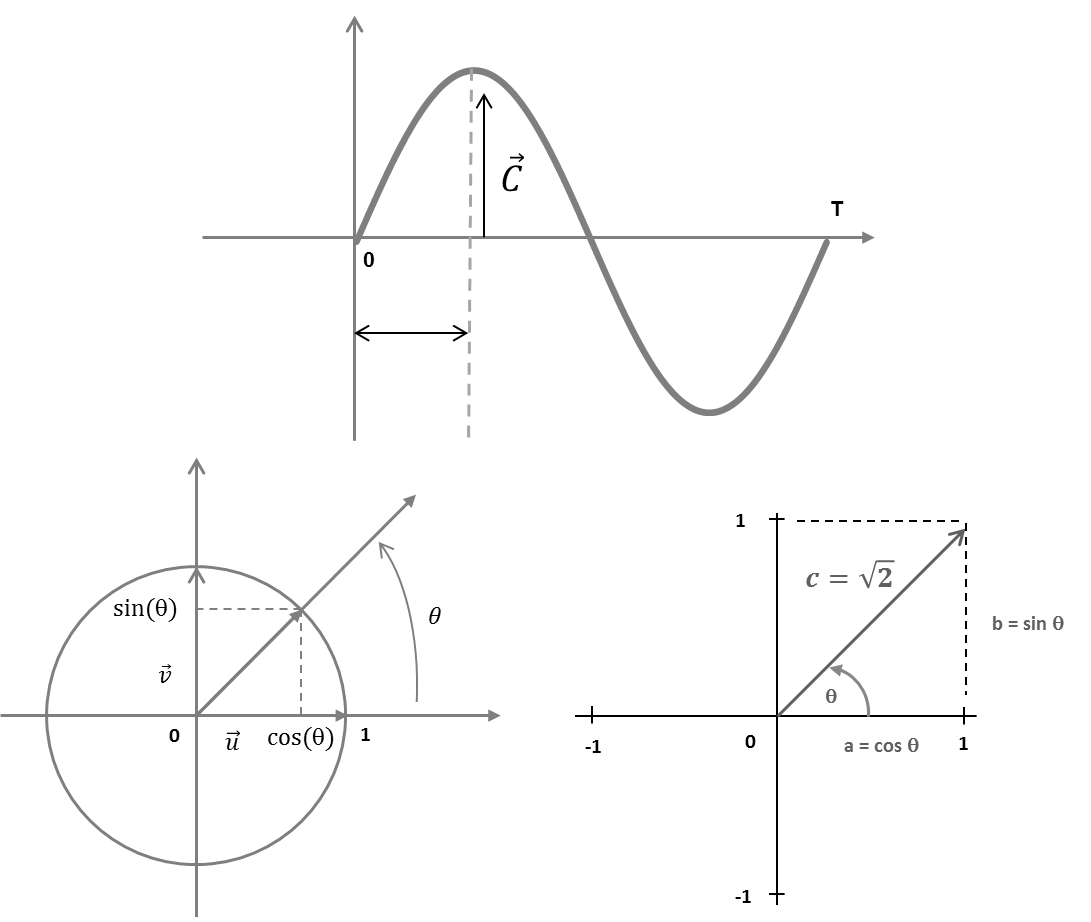
Le vecteur [latex]\overrightarrow{C}[/latex] représente l’amplitude et l’angle [latex]\theta[/latex] représente la phase.
[latex]a^{2}+b^{2}=c^{2}[/latex]
[latex]1^{2}+1^{2}=c^{2}[/latex]
[latex]c^{2}=2[/latex]
[latex]c=\sqrt{2}[/latex]
Les mathématiciens ont simplifié l'approche en admettant que tous les triangles rectangles considérés seraient posés sur un cercle de rayon 1. Le point qui se déplace sur la circonférence du cercle a pour coordonnées [latex]X(\theta)=Cos(\theta)[/latex] et [latex]Y(\theta)=Sin(\theta)[/latex] avec des valeurs pouvant varier dans l'intervalle [latex]\left[-1; +1\right][/latex].
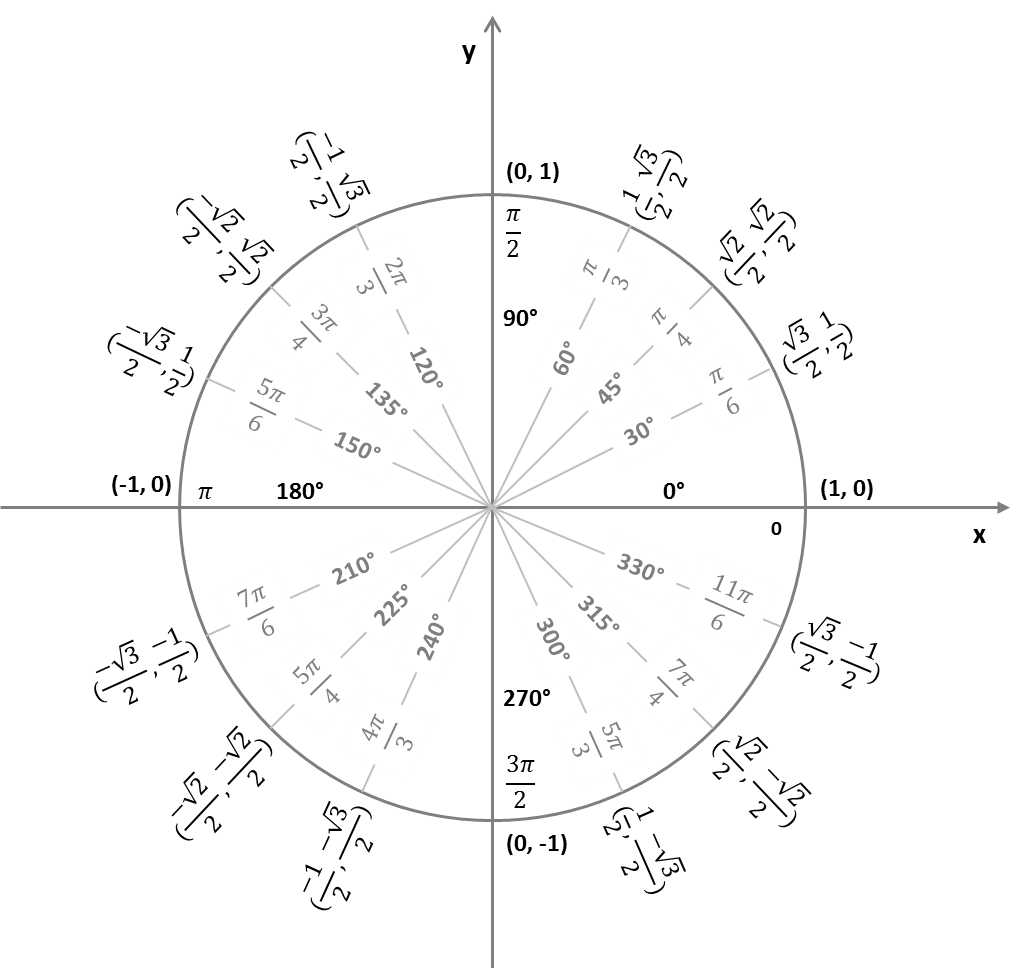
[latex]X(\theta)=Cos(\theta)[/latex] et [latex]Y(\theta)=Sin(\theta)[/latex]
Le radian est une mesure d'angle et une mesure de longueur sur le cercle trigonométrique de rayon 1. La valeur de l'angle [latex]\theta[/latex] en radians est aussi la valeur de la longueur de l'arc de cercle intercepté par l'angle [latex]\theta[/latex].
