8 Robust control

Key Concepts

In this chapter we will:

• Introduce the concept of signals and systems
• Explore a short history of control theory in sustainability
• Map a standard control system and discuss the key concepts of stability and robustness in designed feedback systems.

8.1 Introduction

The word ‘control’ has the connotation that we act on a system to determine an outcome. That is, you are in ‘control’ of your life. You can ‘control’ focus on designed systems.This is anthropocentric. No need to think of ‘control’ with its implied notions of ‘agency’. Why are you trying to ‘control’ something? Because someone or something else is controlling you (hunger, fear, shame, etc.). So let’s forget about control, and think about what it really is: the process of taking some information from a system, using it to make a decision, then acting based on that decision.

This basic idea is captured in Figure 8.1. Information flows around the loop. Somehow the system that is being controlled (the ‘dynamic system’) such as your car, your body, a machine, an ecosystem, and economy, whatever. This dynamic system is referred to as such as it isn’t very interesting to act on a static system. The dynamic system is evaluated by a ‘sensor system’, i.e. is being measured in some way. Your stomach has a sensor system that creates a signal that you interpret as ‘hungry’. This hungry signal enters your ‘evaluation/action system’ and you take action, i.e. go get some food that then feeds back (alters) the dynamic system in some way, i.e. some biomass moves from an ecosystem into your stomach. And this loop functions continuously to keep you in an ‘alive’ state. This ‘alive’ state is an extremely complex state captured by the organization of molecules in your body.

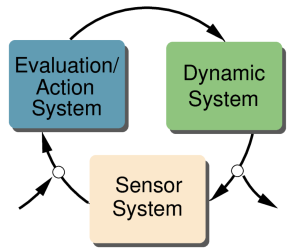
These simple examples illustrate a much deeper point: all persistent structures, any observable pattern, are created and maintained by networks of such simple feedback structures shown in Figure 8.1, depicted in Figure 8.2.

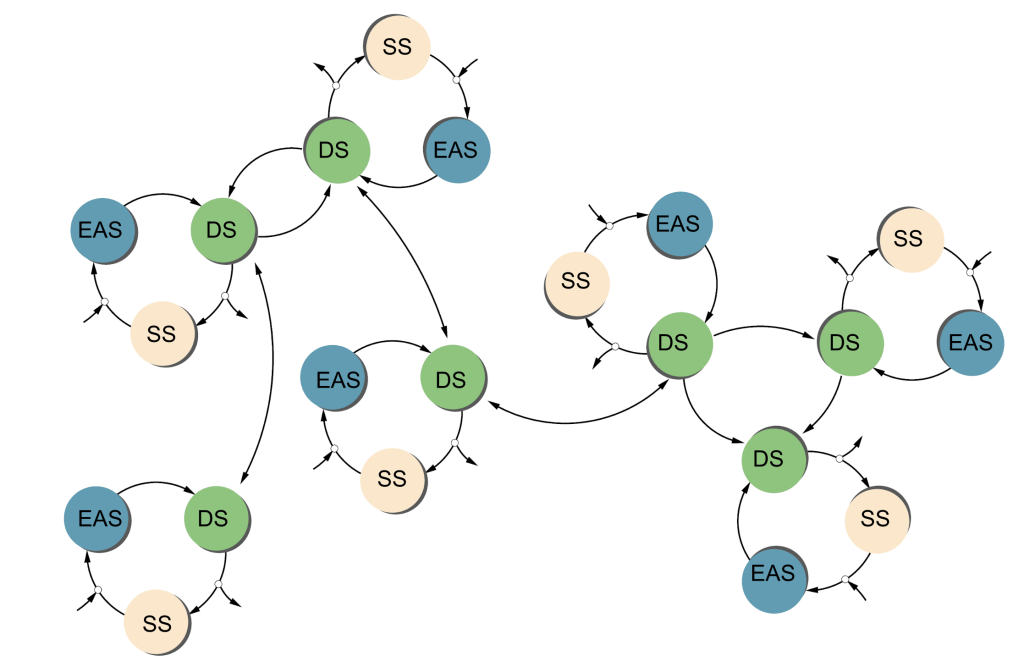
In your body, there is a feedback loop to keep your temperature, your blood sugar level, your balance, etc. within some reasonable range. Together, they produce you as a persistent structure. When one of these loops goes wrong, it can cascade through the whole system and cause catastrophic failure. The idea of “governance” or “policy” or “management” is really about making the rules (institutions) and creating the hardware (organizations, monitoring systems, etc.) to implement those rules.

8.2 Control theory basics

In control theory, there are always four basic components:

1. A goal, e.g. produce a certain flow of resources such as in a sustainable fishery, maintain a system state such as the atmospheric carbon dioxide concentration,
2. A controller, e.g. a mechanism that takes information about the system, compares it with the goal and takes action accordingly,
3. The system being controlled, e.g. an ecosystem, a factory, a car, an airplane, the earth system.
4. A sensor, e.g. a way to measure the system state, e.g. what is the fish biomass in a fishery, what is the water level in an aquifer, what is the carbon dioxide concentration in the atmosphere, what is the phosphorus level in a water body, or system flows, e.g. how many fish are being caught, how much water is being extracted, and how much carbon is being emitted into the atmosphere per unit time.

Figure 8.3 illustrates the “block diagram” depiction of control systems that are common in the controls literature. For a generic control system, the blocks are typically called the ‘controller block’, the ‘plant block’ (think of a manufacturing or a chemical plant), and the sensor block. It doesn’t matter what the blocks are as long as the blocks do what is listed as above. That is, control theory and the block diagram can be applied to any system, from a cell, to your body, to a spaceship.

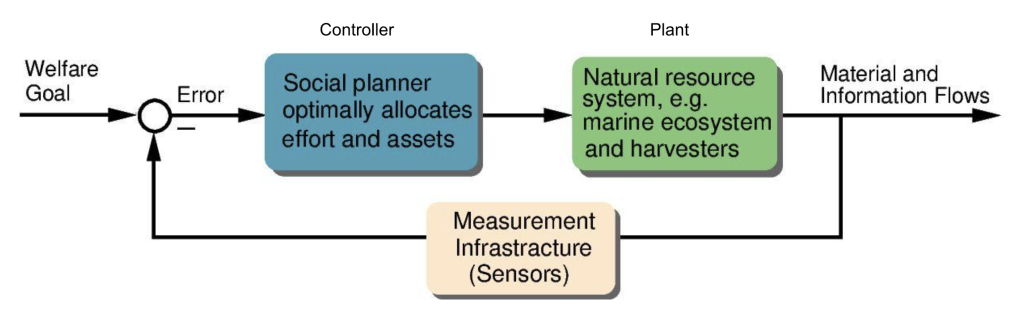
The absolutely essential feature of a control system is that information flows in a loop! Let’s walk through the diagram. First is some information about a goal that flows into the control system. That goal information is compared to information about the recent state of the system. This is the arrow from the sensor that flows into the circle. Usually the ‘comparison’ is the difference between the actual state of the system and the goal state and this difference is the ‘error’. Imagine you set your cruise control in your car at 60. Some sensor in your engine, motor, or wheels senses the speed. Is it 60? Let’s say it is 58. The error = goal – actual = 60 – 58 = 2. So an error of 2 is fed into the controller which has a rule (a policy) that says ‘if the error is positive, accelerate’. Now the signal “accelerate” is sent from the controller block to the plant block. What is the ‘plant’ in this case? The plant is the car and the landscape (the weight of the car and the landscape it is on will determine how it will move naturally without any force from the engine or brakes) and the car’s engine and brakes which provide the control to change the velocity of the car (note that the controls have to match the goal – our goal is velocity and we must be able to change the variable related to the goal).

Let’s now suppose the next reading of the speed is 60 (the plant has done its job to accelerate the car). Then the error is 60-60=0. Zero is fed into the controller. There is a rule in the controller that says “if the error is zero (we have achieved our goal), do nothing, i.e. neither accelerate nor decelerate. Next, suppose as you are driving, you come to a downhill section in the road. Your car naturally wants to accelerate because of gravity – an intrinsic feature of the ‘plant’. Now the sensor detects a speed of 65. Now the error is 60-65=-5. The error of -5 is sent to the controller which has a rule like ‘if the error is negative, decelerate. The signal ‘decelerate’ is then sent to the plant which reduces the throttle to the engine and/or applies the brakes and the car slows down. In this way, an error detection, error correction loop (EDECL) can maintain the goal speed. There are many subtle problems with such EDECLs that must be solved and the methods for doing so are the core off control theory.

In what follows, we will use the ‘car speed control’ example. While it may sound simplistic to attempt to relate the control of complex systems to cruise control in a car, the problems are, in principle, the same. Control is fundamentally about keeping some system in a desired state by speeding it up or slowing it down, i.e. managing a rate or a collection of rates. Think of a fishery. We manage it by speeding up or slowing down the harvest rate. We manage the climate by slowing down the carbon emission rate or slowing it down to negative rates, i.e. removing carbon dioxide from the atmosphere. We manage aquifers by speeding up or slowing down the extraction rate. Groundwater recharge is, of course, slowing the extraction rates to negative levels, i.e. negative extraction is recharge. Thus, in the end, the relatively simple problem of controlling the speed of a vehicle in one direction has the essential features of much more complex control problems. We now explore key challenges and insights from control theory using this example.

8.2.1 System stability

One key problem feedback control must address is stability. That is, can the system hold its state close to the goal? In the car example, if we adjust the control based on the instantaneous error, we cannot reach the goal. Why? Because when the error is zero, the controller doesn’t do anything. Thus, only when the speed moves away from the goal does the controller react. This means that such a controller can only keep the speed within a range of the goal. That is, it will keep accelerating and decelerating as the speed moves up and down. The same is true for your thermostat in your house. You may have noticed that your heater or air conditioner cycles on and off according to what is called the ‘residual’, i.e. the error. Most heating systems have a residual of 2 degrees. So if you set the thermostat at 70 degrees in the summer, the air conditioner will turn on at 72, cool your house to 68 and then turn off. The temperature will then naturally rise to 72 when the thermostat will turn back on. So the temperature in your house will fluctuate between 68 and 72, but will never actually settle at 70. In the case of a home climate management system, this fluctuation is a fundamental property of the heating system: you can only turn a heat pump on and off. You can’t run it at any speed, it only has a limited number of speeds. With the car example, it is due to other factors as we can run the engine at any speed we want and we can brake to any speed we want. Rather, fluctuations are due to something engineers call bandwidth – i.e. how fast the controller and plant can respond.

The bandwidth issue is manifest in physical systems due to inertia. Inertia, in simple terms, is the fact that the energy required to change the velocity of an object depends on its mass and velocity. Quickly changing the velocity of a moving object can require an enormous amount of energy. Thus, the ability of the plant to produce energy fundamentally limits the bandwidth, or speed of response of any system. In the car, this is the horsepower of the engine – i.e. the common advertisement that a car can go from 0-60 mph in so many seconds, and the braking distance (or time). So, no matter how good the controller and sensors are, our capacity to keep a car at a particular speed is limited. On a flat road with no wind, with good controller design, we can keep a car extremely close to the set speed. But we know we can’t just rely on real-time information or we will chase our tail – think of trying to get your shower temperature just right based on how the water temperature feels now. In control theory, the most common type of controller, by far, is called a PID controller. P stands for proportional – you adjust your responses in proportion to the present error. I stands for integral – you adjust your response based on the sum of past errors. Finally, D stands for differential – you adjust your response based on your estimate of how the error is changing – usually the present error minus the previous time step error divided by the time step. This is a measure of future error. Most control strategies are then a weighted sum of P, I, and D strategies. In a perfect world, feedback control loops can be constructed to achieve any goal within the biophysical limits of the plant and limits to how fast the controller can process information. For an example of just how powerful feedback control is in ideal conditions, see this youtube video. Unfortunately, we do not live in a perfect world.

8.2.2 System robustness

Figure 8.3 depicts a control system for ideal conditions. In the imperfect world we live in, we often don’t know how the plant works, the system is exposed to exogenous shocks, we can’t get perfect measurements, and we can’t process information arbitrarily quickly. These factors introduce mistakes and delays into the feedback system which can wreak havoc. Figure 8.4 shows the block diagram for real-world feedback control systems that we face in the real world. First, we can’t even agree on a goal. Do human carbon emissions really contribute to climate change and do we limit carbon emissions or not? What should we limit them to? Are the scientists being overly reactive? Are we really overexploiting global fisheries? Most scientists say yes, others are not so sure. What level of harvest is sustainable? Is present economic inequality too high? Is high inequality good (some say it motivates entrepreneurship) or is it bad (others say it stifles economic growth). What level of inequality is good? What gini coefficient should society shoot for? Should 20 percent of the people be allowed to own 80 percent of the world’s economic assets? And the list goes on and on……

Now, let’s use the car driving example to work our way around the control loop. First, suppose that there is not one, but 5 people in the car who somehow elect a driver. The elected driver may have their own goal about where to go and how fast, but this may not represent the other passengers’ goals. Next, suppose that somehow the group agreed on where to go, and how fast (to the movie at 45 mph). Now suppose after the journey begins, some in the group think that the car is going too fast. They have received some sensor information they believe indicates the car is not going 45. One yells ‘slow down’, the other ‘speed up’. The driver says “but the speedometer is indicating 45”, a third says “I don’t believe the speedometer”. Resolving this disagreement takes time, and introduces a delay between when information is received and when it is acted on, e.g. we are emitting too much carbon dioxide and should have acted 20 years ago. Now it may be too late and, if not too late, much more expensive. Now consider a situation in which the car randomly slows down when the throttle is pushed. Sometimes it randomly turns left when the steering wheel is turned to the right. Sometimes the brakes randomly don’t work. These are examples of uncertainty in the plant. Suppose that the driver attempts to turn left but the passenger grabs the wheel and pulls it to the right. This is an example of an exogenous disturbance on policy actions. Suppose that an extremely strong headwind buffets the car and effectively slows it down as it tries to accelerate. This is an example of an exogenous disturbance on realized outcomes – yes the car is accelerating as per the drivers signal from the throttle, but it can’t do anything about the wind. Finally, suppose that mud is splattered on the windshield by a passing truck and the speedometer stops working correctly. These are exogenous disturbances on measurements.

While the scenarios above may seem far-fetched, many industrial systems must reliably operate in very challenging conditions. The field of robust control focuses on designing feedback control systems for such conditions. In the discussion of PID controllers above, the details are far beyond the scope of this book and we just focused on the main principles of carefully weighing how we use present, past, and future information to achieve system stability. Robust control system design is even more challenging and the details are, again, far beyond the scope of our discussion here. We just want to leave you with to main principles from robust control:

1. With unlimited bandwidth (essentially the capacity to respond instantaneously), it is possible to keep a system operating within an arbitrarily tight interval given limitations on the observability and controllability of the system. That is, we can build extremely robust systems, but this can be costly.
2. Our ability to increase robustness is limited by the intrinsic dynamics of the system. Just like there is a law in physics that energy is conserved, there is a law in robust control that robustness is conserved. That is we can convert energy into different forms, i.e. kinetic or potential energy, but the total amount of energy is fixed. Similarly, we can spread robustness across different kinds of shocks, but the total ‘amount’ of robustness is fixed. In practical terms, we can direct robustness capacity toward reducing the sensitivity of the system to high frequency variations, but then the system will become vulnerable (very sensitive) to low frequency variations.

So, in summary, we have illustrated the main ideas from control theory: balancing the use of present, past, and future information to achieve stability and using rapidly responding feedbacks to counter certain kinds of shocks to the system knowing that this will cost in terms of weakening the capacity of the system to deal with different kinds of shocks. For an excellent example of the application of these ideas to managing the COVID-19 pandemic, see this youtube video. What do these ideas mean for sustainability more broadly?

8.3 Control theory, governance, and sustainability science

Buckminster Fuller was a futurist and inventor who popularized the term ‘spaceship earth’. Kenneth Boulding then wrote an essay titled “The Economics of the Coming Spaceship Earth” in 1966. Well, at the time of writing of this book some 60 years later, the coming spaceship earth has arrived. If we think of Earth as a spaceship (and it is easy to make this analogy as we do below), then we can see how the example of keeping a car at a certain speed is quite general. The only difference is that when we pilot spaceship earth, the goal is not keep a certain speed but, rather, keep other variables within a ‘safe operating space’ while maintaining a certain level of human welfare. If one considers one aspect of the choice of speed of a car one of a safe speed, then the cruise control system of your car keeps the speed in a safe operating space while maintaining a certain level of the driver’s and passenger’s (the society in the context of transportation in a car) welfare measured in terms of the subjective feelings of the passengers about how long their journey will take. So, again, we see the similarity between the relatively simple problem of controlling speed to that of sustainability, or in other words, controlling spaceship earth.

With humanity’s departure from the Holocene wherein humans predominantly adapted to global dynamics and entrance into the Anthropocene wherein we increasingly control them, we have transitioned from being passengers on to piloting `Spaceship Earth’. As pilots, we become responsible for the life support systems on our `Earth-class’ spaceship. Until very recently Spaceship Earth has been running on autopilot regulated by global feedback processes that emerged over time through the interplay between climatic, geo-physical, and biological processes. These processes must necessarily have the capacity to function in spite of variability and natural disturbances and thus have developed some level of resilience in the classic sense of Holling–the ability to absorb and recover from perturbations while maintaining systemic features.

The capacity of these regulatory feedback networks to provide system resilience is limited. The Planetary Boundaries framework makes these limitations explicit and defines, in principle, a safe operating envelope for Spaceship Earth. The pilots face two challenges: knowing the location of the `default’ operating envelope boundaries and understanding how these boundaries change with changing operating conditions. Pilots typically have an operating manual that provides this information which enables them to better utilize the resilience of their vessel (Earth System resilience). Because we don’t have that luxury, the concept of resilience becomes critical: the art of maintaining life support systems under high levels of uncertainty–flying our Earth-class spaceship without an operating manual. Earth System science is, at its core, the enterprise of uncovering the operating manual. Unfortunately, our capacity to experiment is quite limited: the time required is enormous and the number of independent copies of Earth is limited. We can’t test resilience by transgressing global thresholds and observing how the system behaves in new states and potentially recovers, e.g. `snow-ball Earth’ and the `tropical states’ of Earth’s past.

With a manual, a crew, and a captain, the `resilience’ question would boil down to the competence and risk aversion of the captain and the competence of the crew. This resilience would encompass

• piloting the spaceship so as to avoid shocks (e.g. avoid asteroids, maintain safe speeds, etc.),
• developing knowledge/skills to quickly repair existing systems if shocks can’t be avoided,
• the capacity to improvise and create new systems when existing systems can’t be repaired,
• and conducting routine maintenance so as not to destroy the ship through usage.

The first two elements constitute a key element of robustness, or specified resilience, described above. The third element (general resilience) is much more difficult to invest in. It requires the development of generalized knowledge and process to cope with rare and difficult-to-predict events. The fourth element has been the focus of most environmental policy thus far with a tendency to do just enough to get by.

Now consider our Earth-class spaceship. There is no captain or crew (there is no driver of the car – we all know the problem of the backseat driver). Subgroups of passengers are restricted to certain areas (e.g. the upper or lower decks). Some groups have access to more ship amenities and those with less access often support the production of amenities for those with more. As with the Titanic, the impact of shocks is very different for first- and second-class passengers. There is minimal maintenance of life support systems and, in particular, the waste management subsystem. Complaints about life support systems are met with agreements that it should be fixed but disagreements about who should pay. Worse yet, there is no operating manual so no one knows how to effect repairs, or their costs. No one knows how to set the cruise control, and no one knows how to fix the engine or brakes if they fail.

To an outside observer, our situation might seem absurd – like a crazy group of people in a car arguing about where to go and how fast to go there while the car is careening toward a cliff. If given the choice, many rational passengers on board would disembark. While some extremely wealthy passengers seem to be making an attempt, disembarkation is not realistic. So what do the passengers do? One key difference between the spaceship metaphor and our journey is that there is no destination. Further, the ship’s journey is much longer than our lives so the ship becomes our home. `Good piloting’ is tantamount to effectively managing life support systems–the `Earth System’ (ES)–while ensuring the wellbeing of and preventing critical conflict among the passengers–managing the `World System’ (WS). And because we must do this without an operating manual, we must build World–Earth System (WES) resilience (WER). We must be able to define WER to characterize how close these critical systems are to breaking down and model it to explore mechanisms that enhance or degrade WER.

So, based on what we know about control theory, what considerations should be built into our policies?

8.4 Critical reflections

Robust control is a concept from engineering, but can be applied to other types of systems too. Suppose we wish to navigate the system towards a certain goal (e.g. 60 miles/hour, BMI < 25, net zero carbon emissions), we need to take actions to reach that goal. Due to imperfect understanding of the system and external events, we receive information that indicates we have to adjust our actions to reach our goal.

A robust control perspective can be applied to governance, explicitly acknowledging that we do not have perfect knowledge, and have to create error-detection-error-correction type policies so we keep on track of our collective goals. Goals can only be in reach if we have the bandwidth to make adjustments to the “speed” at which the system changes. We also have to make tradeoffs regarding which kind of disturbances to prepare for, since there is only limited bandwidth available. In Chapter 14 we will discuss the bandwidth problem for reaching net zero carbon emissions by 2050.

8.5 Make yourself think

1. Do you have any ‘robust’ policies in your life? I.e. setting your alarm clock 30 minutes early to make sure you get up in time (your body has ‘sleep inertia’, right?)
2. Try to think of one critical feedback system in your body that regulates some important quantity. There are many to choose from!