Student Learning Objectives

• Determine the payback period for an investment
• Compute the internal rate of return for an investment
• Compute the simple rate of return for an investment
• Find the present value of a sum of money using present value tables
• Evaluate the acceptability of an investment project using the net present value method

Capital budgeting decision making

Managers are responsible for many decisions, some of which have short-term effects and others that have long-term effects.  Projects and investments that have a long-term effect are referred to as capital projects. Therefore, capital budgeting refers to the process of planning projects or decisions that have a long-term impact on the organization.  Examples of capital projects include investments in long-term assets such as vehicles, machines, facilities, or equipment; launching new products or services; and expanding operations.

Capital budgeting decision making is a critical managerial skill.  Most organizations have a limited amount of resources and more potential long-term investments than they can fund. For this reason, managers must have the ability to evaluate the alternatives and select the projects that offer the most benefit to the organization. The ability to select appropriate capital investments is an essential component of an organization’s long-term financial health and stability.

This chapter discusses four methods for making capital budgeting decisions—the payback method, the simple rate of return method, the internal rate of return method, and the net present value method.

Payback period

The payback period is the length of time that it takes for a project to recover its initial cost from the net cash inflows generated by the project. The payback period is expressed in years. The formula to compute the payback period includes the following inputs:

Investment required. The required investment is the cost of the project less the trade-in or salvage value on any assets exchanged in the transaction. For example, assume that Jill decides to purchase a new car for $12,000.  She receives $3,000 for trading in her old car.  The required investment in the new car is $12,000 – 3,000 = $9,000.

Annual net cash inflow. Annual net cash inflow is the net cash inflows yielded by the investment.  It is important to note that both revenue and costs savings are considered cash inflows. When considering an investment that generates both revenue and costs the annual net cash inflow would be cash revenue less cash expenses.  Annual net cash inflow is not the same as net income although they are similar.  Net income includes some non-cash expenses like depreciation, which is an allocation of the cost of a long-term asset and not a cash payment.  Since this method uses annual net cash inflow, depreciation is not considered for this calculation. If net income is given, depreciation expense must be added back to arrive at annual net cash inflow.

When annual net cash inflow is the same every year, the following formula can be used to compute the payback period:

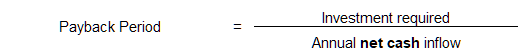
The payback period tool is often used as an investment screening tool and not as a final selection method.  The advantage of this method is that it can be used to quickly screen a number of competing projects. For example, some organizations prefer to invest in projects in which the investment is recovered within a specified period such as 3 to 5 years.  Therefore, this tool can be used to separate out the investments that meet certain payback criteria.

The disadvantages of this tool; however, are significant.  First, this method does not consider the actual profitability of a project.  And second, this method does not consider the time value of money.  The time value of money is the concept that money available today is inherently worth more than an identical amount of money at some time in the future. The time value of money is explored in more detail later in this chapter.

Simple rate of return

The simple rate of return is a quick method to compute an estimated rate of return for an investment or project.  The formula to compute the simple rate of return includes the following inputs:

Investment required. The required investment is the cost of the project less the trade-in or salvage value on any assets exchanged in the transaction.  The investment required is the same input used for the payback period.  Recall the example in which Jill decides to purchase a new car for $12,000.  She receives $3,000 for trading in her old car. The required investment in the new car is $12,000 – 3,000 = $9,000.

Annual net operating income.  The annual net operating income resents the revenues less the expenses yielded by the investment. Since this method uses annual net operating income, depreciation is considered for this calculation. If annual net cash flow is given, depreciation expense is calculated and subtracted from annual net cash flow to arrive at net operating income.

The following formula can be used to compute the simple rate of return:

The simple rate of return tool is often used as an investment screening tool and not as a final selection method.  The advantage of this method is that it can be used to quickly screen a number of competing projects. For example, some organizations prefer to invest in projects that have a minimum rate of return.  Therefore, this tool can be used to separate out the investments that met a minimum rate of return.

The disadvantages of this tool; however, are significant.  First, this method assumes that the revenue and expenses generated by the investment are constant over the life of the project.  This is rarely the case. And second, this method does not consider the time value of money.  As mentioned in the preceding section, the time value of money is the concept that money available today is inherently worth more than an identical amount of money at some time in the future.

Video Illustration 1: Payback period and simple rate of return illustrated

Isabella owns a small machine shop that develops prototypes for metal products. She would like to purchase a new machine capable of creating custom steel tools. She is considered two different models.

The A model would cost $420,000, generate $260,000 in annual cash revenues, and $120,000 in annual cash operating costs. The A model has a 10 year useful life.

The B model would cost $360,000, generate $180,000 in annual cash revenues, and $60,000 in annual cash operating cost. The B model has an 8 year useful life.

Compute the payback period and simple rate of return for both machines.

Time value of money

The time value of money is the concept that money available today is inherently worth more than an identical amount of money at some time in the future. For example, $1,000,000 payable today is inherently worth more than $1,000,000 paid at the end of the year.  There are two financial reasons for this. The first factor is the concept of inflation. Inflation is an economic concept that measures the general increase in prices and the resulting decline in the purchasing value of money over a period of time. Generally, inflation occurs gradually over a long period of time so it is ignored in most capital budgeting decisions.

The second reason is relevant to capital budgeting decisions.  Money today is worth more than money in the future because it can be used today to generate interest or a return. For example, $1,000,000 today can be invested in an interest-bearing investment or in an organizational project to yield a return on that investment. Assume that the $1,000,000 can be invested in a savings accounting yielding 3% interest.  In this case, $1,000,000 today becomes $1,000,000 x 1.03 = $1,030,000 one year from now.  Or, a business could invest the $1,000,000 in a new product that yields a 15% return in which the money would be worth $1,150,000 one year from now.

Since the formula to calculate interest is constant (principle x rate x time), mathematical tables have been developed to determine the present value discount factors for a number of different interest or return rates as well as a number of time periods. There are two types of present value calculations.

Present value of a lump sum.  The present value of a lump sum, often referred to as the present value of 1, is the present value of a single cash flow at some future point.  For example, a company will receive $10,000 when they sell the machine in 10 years.  This is a single cash flow of $10,000 that happens one time 10 years from now.

Present value of an annuity.  An annuity is simply a series of equal payments.  This is not a single or lump sum payment but a series of equal payments.  For example, the settlement ordered annual payments of $100,000 per year for 5 years.  This is an annuity.  The total amount of cash is $500,000 (5 payments x $100,000). However, it is not really worth $500,000 since it is not all received now. The cash received in the second year is worth less than the cash received in the first year.  And the cash received in the fifth year is worth less than the cash received in the first four years.

The present value of a lump sum and the present value of an annuity discount tables are presented in the Appendix.  These tables can be used to easily determine the present value of a future lump sum or annuity amount. To find the present value, the future amount is multiplied by the discount factor for the corresponding interest rate and time period.

Internal rate of return

The internal rate of return method is similar to the simple rate of return with one major difference.  This method takes into consideration the time value of money.  This method calculates the discounted rate of return of an investment over the useful life of the investment. The formula to compute the internal rate of return includes the following inputs:

Investment required. The required investment is the cost of the project less the trade-in or salvage value on any assets exchanged in the transaction. The investment required is the same input used for the payback period and the simple rate of return.  Recall the example in which Jill decides to purchase a new car for $12,000.  She receives $3,000 for trading in her old car. The required investment in the new car is $12,000 – 3,000 = $9,000.

Annual net cash inflow. Annual net cash inflow is the net cash inflows yielded by the investment. This is the same input used by the payback period.  It is important to note that both revenue and costs savings are considered cash inflows. When considering an investment that generates both revenue and costs the annual net cash inflow would be cash revenue less cash expenses. Since this method uses annual net cash inflow, depreciation is not considered for this calculation. If net income is given, depreciation expense must be added back to arrive at annual net cash inflow.

The following formula can be used to compute the internal rate of return:

To find the internal rate of return the discount factor is located on the present value of an annuity discount table (Appendix A: Present Value Tables) in the row matching the useful life of the project.  The corresponding rate of return is the internal rate of return.  This is the rate at which the present value of the project is discounted to zero since the discounted amount includes the rate of return.

The advantage of this method over the payback method or the simple rate of return method is that it considers the time value of money.  The major disadvantage is that this method only works for investments with a single cash investment at the beginning and constant cash flows over the life of the investment.  Many capital budgeting projects require multiple investments at different times during the project and produce uneven cash flows over the life of the investment.

Video Illustration 2:  Internal rate of return

Paula is thinking about replacing her stitching machine. A new machine would cost $130,000.  She would receive $6,000 for trading in her old machine. The new machine would generate $52,000 in annual revenue and $27,000 in annual cash expenses. The new machine has an 8 year useful life.

What is the internal rate of return for the new stitching machine?

Net present value method (NPV)

Like the internal rate of return, the net present value method also considers the time value of money.  Unlike the internal rate of return method, the net present value method can be used to evaluate investments where multiple cash investments are required and the project has uneven cash flows over the life of the investment.

The net present value method compares the present value of a project’s cash inflows to the present value of its cash outflows at a predetermined discount rate.  The discount rate is the minimum rate of return established by the organization.  All of the cash inflows and outflows of the investment are discounted at this rate.  Discounted cash inflows are positive and discounted cash outflows are negative. The discounted cash flows are then netted together to produce the net present value of the investment.

A positive net present value means that the return on the investment is greater than the discount rate.  Or, that the investment will yield a higher return than the discount rate.  For example, if the net present value is positive and the discount rate used was 12%, the project returns more than 12%. Although the exact return is not provided by this tool, a positive value means that the return is more than 12%.

A zero net present value means that the return on the investment is equal to the discount rate. This does not mean the investment has a zero return.  The cash flows were discounted at a specific rate so the investment returns exactly that rate. For example, if the net present value is zero and the discount rate used was 12%, the project returns exactly 12%.

A negative net present value means that the return on the investment is less than the discount rate.  Or, that the investment will yield a lower return than the discount rate.  This does not mean that the investment does not generate a return. Instead, it means that the return is less than the discount rate.  For example, if the net present value is negative and the discount rate used was 12%, the project returns less than 12%. Although the exact return is not provided by this tool, a negative value means that the return is less than 12%.

Video Illustration 3:  Net present value method

Jen Labs is considering the purchase of a new lab machine to test blood samples for specific viruses.  The machine costs $372,000.  The machine has a useful life of 6 years.  The machine will require a $50,000 general maintenance service in year 3.  If they purchase this machine, they estimate that they will run 1,500 blood tests per year.  They can charge $120 per blood test.  The machine will require $81,000 per year in operating costs. At the end of the six years, the machine has a $24,000 trade-in value.  Jen Labs requires a minimum return of 10% on all investments.

Compute the net present value of this investment using  Appendix A: Present Value Tables.

Practice Video Problems

Practice Video Problem 1: Payback period, simple rate of return, and internal rate of return

Holly Rich is considering becoming an independent contractor for a national rideshare company as a second job. Her current car is older and not reliable enough to use for the business. She is considering purchasing a newer car to use in the business.  A reliable used car would cost $19,000.  The dealer offered her $1,000 trade-in value on her old car.  The trade-in will be applied to the purchase of the new car. The car will have a 5-year useful life.  She estimates that she can provide 40 rides per week and work 50 weeks per year.  She earns an average of $9 per ride.  Her cash expenses average $6.50 per ride.  Annual depreciation on the car would be $3,800 per year.

Required: Compute the payback period, simple rate of return, and internal rate of return for this investment.

Payback period

Simple rate of return

Internal rate of return

Practice Video Problem 2: Net present value method

The manager of Quick Print, Inc. wants to replace an outdated, large-format analog printer.  She has narrowed the decision down to two digital models, the standard commercial model or the premium commercial model.  The required minimum rate of return on all investments is 12%.

The standard model costs $72,000 and has a useful life of 6 years.  The standard model requires maintenance service in year 2 and year 4 at a cost of $2,100 per service.  Annual revenue is estimated to be $36,000 and annual cash operating expenses are estimated to be $12,000.  The salvage value is estimated to be $7,200.

The premium model cost $93,000 and has a useful life of 8 years.  The premium model requires maintenance service in year 2, year 4, and year 6 at a cost of $2,100 per service. This copier can be used to provide more services than the standard model so annual revenue is estimated to be $52,000 and annual cash operating expenses are estimated to be $21,000.  The salvage value is estimated to be $5,200.

Required: Compute the net present value for both copiers using Appendix A: Present Value Tables.