Hoofdstuk 6.2: Beschrijvende en toetsende statistiek
Sylvia Jansen
abstract
Dit hoofdstuk gaat in op de belangrijkste aandachtspunten bij het uitvoeren van een beschrijvende of toetsende analyse. Onderwerpen die worden besproken zijn onder meer toevalsfluctuaties en hypothesetoetsing.
Introductie
“De gemiddelde prijs van woningen blijft stijgen” (NOS 2020)
“Huurders minder tevreden met hun woning” (CBS 2019)
Zomaar twee voorbeelden uit het nieuws. Hoe weten we dat de gemiddelde prijs van woningen blijft stijgen of dat huurders minder tevreden zijn met hun woning? Je kunt dit op een kwalitatieve manier onderzoeken, bijvoorbeeld door makelaars en huurders te interviewen of door krantenartikelen te verzamelen en de inhoud ervan te analyseren. Maar je kunt dit ook op een kwantitatieve manier doen door numerieke data te verzamelen en te analyseren. In het laatste geval gebruik je daarvoor beschrijvende en toetsende statistiek.
Beschrijvende en toetsende statistiek
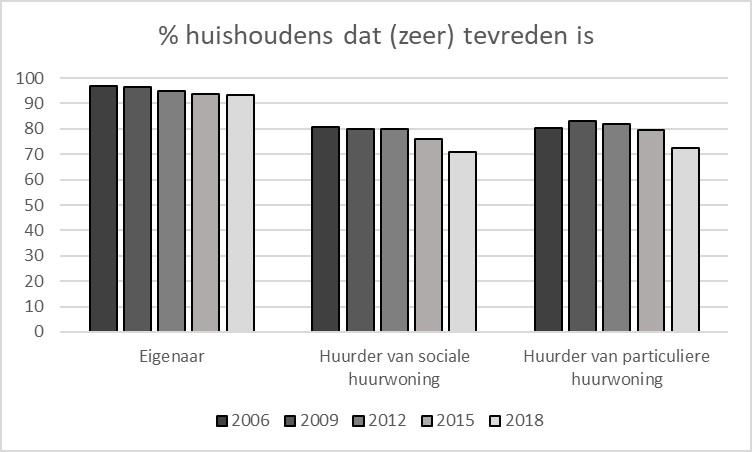
Bij beschrijvende statistiek gaat het om een beschrijving van de dataset. Dat kan data zijn die je daadwerkelijk zelf hebt verzameld, bijvoorbeeld door middel van een enquête. Maar het kan ook zijn dat je gebruik maakt van een al bestaande dataset die door iemand anders is verzameld. Je kunt de data beschrijven door bijvoorbeeld het gemiddelde te berekenen en de laagste en de hoogste waarde te presenteren. Of je kunt met behulp van een staafdiagram laten zien hoeveel respondenten een bepaald antwoord hebben gegeven. Uit figuur 6.2.1 kan bijvoorbeeld afgelezen worden dat 81 procent van de ondervraagde huurders van een sociale huurwoning in 2006 (zeer) tevreden was met de woning. Dit percentage daalde in 2012 en in 2015. In 2018 was het percentage (zeer) tevreden bewoners nog maar 71 procent. Dit voorbeeld is gebaseerd op het WoON onderzoek 2018 dat is uitgevoerd door het CBS in samenwerking met het Ministerie van Binnenlandse Zaken en Koninkrijksrelaties. Het onderzoek is uitgevoerd bij zo’n 68.000 respondenten in Nederland waarvan maar een deel huurder is.
Bij toetsende statistiek willen we uitspraken doen over een bepaalde populatie op basis van de data waarover we de beschikking hebben. Sommige onderzoekers hebben daadwerkelijk de beschikking over alle cases waarvoor het onderzoek relevant is. We noemen dit de populatie. De meeste onderzoekers hebben echter maar een selectie van cases uit de totale populatie. Dit geldt bijvoorbeeld ook voor het hiervoor genoemde WoON 2018 onderzoek.
Het CBS rapporteert dat er in 2018 geen verschil is tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning voor wat betreft de tevredenheid met de woning (CBS 2019). Toch zie je in Figuur 6.2.1 dat er wel een klein verschil is in de tevredenheid tussen huurders van een sociale huurwoning en huurders van een particuliere huurwoning. Hoe kan dat nu? Zo’n verschil kan veroorzaakt zijn door toeval. Dit onderwerp wordt in de volgende paragraaf verder toegelicht. Bij toetsende statistiek wordt onderzocht of een eventueel verschil tussen twee (of meer groepen) in een steekproef het resultaat is van toeval of dat het een systematisch (echt) verschil betreft dat ook in de populatie aanwezig is. In het huidige voorbeeld gaat het erom of het kleine verschil dat tussen de twee typen huurders in de respondentgroep wordt gevonden, duidt op een echt verschil in tevredenheid tussen alle huurders van een sociale huurwoning en alle huurders van een particuliere huurwoning in Nederland. Volgens de informatie van het CBS is dat niet het geval.
Onnauwkeurigheid door toevalsfluctuatie
De respondenten die door het CBS zijn ondervraagd, zijn “random” geselecteerd. Dat wil zeggen dat alle geschikte potentiele respondenten in principe dezelfde kans hadden om in de steekproef terecht te komen. Maar je kunt je vast wel voorstellen dat als er toevallig een andere groep van respondenten zou zijn geselecteerd de resultaten (bijvoorbeeld de tevredenheid met de woning) net even iets anders zouden zijn geweest. Dat noemen we toevalsfluctuaties. Dit heeft als gevolg dat er een onnauwkeurigheid zit in de uitspraken (schattingen) die je doet op basis van de data. Het kan zijn dat de in het onderzoek geselecteerde huurders van een sociale huurwoning in 2018 toevallig net even iets negatiever waren over hun woontevredenheid dan de hele populatie van huurders van een sociale huurwoning in Nederland.
Hoe weet je nu of er sprake is van een echt verschil in woontevredenheid (een systematisch verschil) of dat het verschil een toevalsfluctuatie is? Hier gebruiken we toetsende statistiek voor. Met behulp van de toetsende statistiek wordt op basis van de al aanwezige spreiding in de antwoorden een schatting gemaakt van het verschil dat we zouden kunnen verwachten op basis van toeval. Met de “al aanwezige spreiding” wordt bedoeld dat de respondenten onderling verschillen in hun antwoorden; in dit voorbeeld de mate van tevredenheid met de woning. Indien het werkelijk gevonden verschil groter is dan het verschil dat we op basis van toeval kunnen verwachten, dan is er dus sprake van een systematisch – en dus “echt” – verschil. Hoe gaat het dat nu precies in zijn werk? De volgende paragraaf gaat daar dieper op in.
Hypothesetoetsing
Wellicht heb je wel eens gehoord van het al dan niet verwerpen van hypothesen in de statistiek. Voor het uitvoeren van toetsende statistiek wordt gebruik gemaakt van hypothesen. Het uitgangspunt van een statistische analyse is dat er “geen effect” is. Dat wil zeggen dat er van tevoren wordt verondersteld dat er geen verschil is tussen twee of meer groepen of dat er geen samenhang is tussen twee of meer variabelen. Er wordt bijvoorbeeld aangenomen dat er geen verschil is in de tevredenheid met de woning tussen de huurders van een sociale huurwoning en de huurders van een particuliere huurwoning. Of er wordt verondersteld dat er geen samenhang is tussen de variabelen leeftijd en tevredenheid met de woning. We noemen deze hypothese van “geen effect” de nulhypothese. Daarnaast is er een zogenaamde alternatieve hypothese. De alternatieve hypothese stelt dat er wèl een effect is. Er wordt bijvoorbeeld aangenomen dat er wel een verschil is in de tevredenheid met de woning tussen de huurders van een sociale huurwoning en die van een particuliere huurwoning. Of er wordt verondersteld dat er wel een samenhang is tussen de leeftijd en de tevredenheid met de woning (bijvoorbeeld hoe ouder men is, des te meer is men tevreden met de woning). Als je bijvoorbeeld zou willen onderzoeken of in 2018 de huurders van een particuliere huurwoning even tevreden zijn met hun woning als de huurders van een sociale huurwoning, dan zou je de volgende hypothesen hanteren:
H0: Er is geen verschil in de tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning
H1: Er is een verschil in de tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning
Het idee achter de hypothesetoetsing is dat de onderzoeker probeert om de nulhypothese te weerleggen op basis van de resultaten van de statistische analyse. Als dat niet lukt, dan stelt de onderzoeker dat “de nulhypothese niet verworpen kan worden”. Dat betekent dat er wordt aangenomen dat er geen effect is (geen verschil of geen samenhang). Indien de nulhypothese wel verworpen kan worden, dan stelt de onderzoeker dat het aannemelijk is dat er een effect is (een verschil of een samenhang). Maar hoe gaat dat verwerpen nu eigenlijk in zijn werk? Een gedetailleerde beschrijving daarvan voert te ver voor dit hoofdstuk. Een heldere (en humoristische) uitleg kan bijvoorbeeld hier gevonden worden: www.youtube.com/watch?v=-MKT3yLDkqk
P-waarde
Om te onderzoeken of er een verschil is tussen twee (of meer) groepen of een samenhang tussen twee (of meer) variabelen kan een statistische toets uitgevoerd worden. Een overzicht van een aantal vaak gebruikte statistische toetsen wordt in tabel 6.2.1 gegeven. Hierbij is het belangrijk om te denken aan het hiervoor gemaakte onderscheid tussen steekproef en populatie. De statistische toets wordt uitgevoerd op de steekproef en met het resultaat ervan hoopt de onderzoeker iets te kunnen zeggen over de populatie. Denk aan bovenstaand voorbeeld over het verschil in de tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning. Er zijn vier situaties mogelijk:
- De onderzoeker vindt een verschil in de tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning in de steekproef en concludeert dat er over het algemeen een verschil is. In de (theoretische) populatie is er ook een verschil. Dus dit is een correcte conclusie.
- De onderzoeker vindt een verschil in de tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning in de steekproef en concludeert dat er over het algemeen een verschil is. In de (theoretische) populatie is er echter geen verschil. We noemen dit een type 1 fout.
- De onderzoeker vindt geen verschil in tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning in de steekproef en concludeert dat er over het algemeen geen verschil is. In de (theoretische) populatie is er ook geen verschil. Dus dit is een correcte conclusie.
- De onderzoeker vindt geen verschil in tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning in de steekproef en concludeert dat er over het algemeen geen verschil is. In de (theoretische) populatie is er echter wel een verschil. We noemen dit een type 2 fout.
Je ziet dus dat er de mogelijkheid is dat de onderzoeker een verkeerde conclusie doet op basis van de resultaten van de statistische toets die wordt uitgevoerd in de steekproef. Elke statistische toets die wordt uitgevoerd, levert een bepaalde numerieke waarde op (een resultaat) en een daaraan gelinkte p-waarde. De p in p-waarde staat voor “probability”. De p-waarde geeft de kans aan dat de nulhypothese (de hypothese van “geen effect”) ten onrechte wordt verworpen. De p-waarde kan een waarde aannemen tussen 0 en 1 (anders gesteld: tussen 0 en 100%). Hoe dichter de waarde bij 0 ligt, des te kleiner is de kans dat de nulhypothese ten onrechte verworpen wordt. In andere woorden, een zeer lage p-waarde suggereert dat er een verschil is tussen twee (of meer) groepen of dat er een samenhang is tussen twee (of meer) variabelen. Maar bij welke waarde van p kunnen we nu zeggen dat er een effect is? Over het algemeen wordt een grenswaarde van 5% gehanteerd (notatie: α = 0.05). Ligt de gevonden p-waarde onder de 5% grens (dus p < 0.05), dan wordt de nulhypothese verworpen ten gunste van de alternatieve hypothese. Er wordt dan gesteld dat er een effect (verschil of samenhang) is in de populatie. Maar bedenk dat er een kleine kans is (< 5%) dat zo’n resultaat gevonden wordt terwijl er geen sprake is van een effect in de populatie (type 1 fout). Bij een p-waarde boven de 5% wordt de nulhypothese niet verworpen. Maar ook dan kan een verkeerde beslissing genomen worden: de nulhypothese kan namelijk ten onrechte niet verworpen worden. In de steekproef wordt dan geen effect gevonden, maar in de populatie is er wel degelijk een effect (type 2 fout).
Veel gebruikte statistische toetsen
Hierboven werd kort de statistische toets aangestipt om te onderzoeken of er een verschil is tussen groepen of een samenhang tussen variabelen. Het aanbod aan statistische toetsen is groot. Voor meer uitleg over de verschillende technieken, zie bijvoorbeeld Baarda et al (2014), Field (2018) en Saunders et al (2019). Tabel 6.2.1 laat een overzicht zien van een aantal veel gebruikte statistische toetsen. Welke toets het meest geschikt is, is onder meer afhankelijk van 1) het meetniveau van de data, 2) het type onderzoek (verschil of samenhang), 3) het aantal groepen of variabelen (1, 2 of meer dan 2 groepen) en 4) of de onderzochte groepen al dan niet afhankelijk zijn van elkaar.
Het meetniveau is het onderwerp van de laatste paragraaf van dit hoofdstuk. Het type onderzoek wordt bepaald door de onderzoeksvraag. Is er sprake van een onderzoek naar een verschil tussen twee (of meer) groepen, bijvoorbeeld het verschil in tevredenheid tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning? Of is er sprake van een onderzoek naar de samenhang tussen twee (of meer) variabelen, zoals bijvoorbeeld de samenhang tussen leeftijd en de tevredenheid met de woning (bijvoorbeeld: neemt de tevredenheid met de woning toe met de leeftijd)? Het aantal groepen of variabelen (1, 2 of meer) spreekt voor zich. Zo is er bij het hiervoor genoemde onderzoek naar een verschil in tevredenheid met de woning tussen huurders van een particuliere huurwoning en huurders van een sociale huurwoning sprake van twee groepen (dus: twee typen huurders). Als vierde punt werd de (on)afhankelijkheid van de te onderzoeken groepen genoemd. Groepen zijn onafhankelijk van elkaar als de onderzoekseenheden waaruit de beide groepen bestaan maar in één van de twee groepen voorkomen en er geen relatie tussen de onderzoekseenheden van beide groepen is. Bijvoorbeeld, een respondent kan op één moment huurder zijn van een particuliere huurwoning of van een sociale huurwoning, maar niet allebei tegelijk. Een voorbeeld van een onderzoek met gerelateerde groepen is wanneer dezelfde huurder van een particuliere huurwoning op twee verschillende momenten, bijvoorbeeld in 2015 en 2018, naar de tevredenheid met de woning gevraagd wordt. Voor het onderzoek naar zulke gerelateerde groepen worden andere statistische toetsen gebruikt, die hieronder niet genoemd worden.
| Type onderzoek
|
Toets |
| Samenhang tussen twee variabelen | |
| Nominaal meetniveau | Chi2 toets |
| Ordinaal meetniveau | Spearman correlatie |
| Interval of ratio meetniveau | Pearson correlatie |
| Samenhang tussen meer dan twee variabelen | |
| Afhankelijke: interval of ratio meetniveau
Predictoren: interval of ratio meetniveau of bivariaat (2 categorieën) |
Regressie analyse |
| Verschil tussen twee onafhankelijk groepen | |
| Nominaal meetniveau | Chi2 toets |
| Ordinaal meetniveau | Mann-Whitney U test |
| Interval of ratio meetniveau | Independent samples t-test |
| Verschil tussen meer dan 2 onafhankelijke groepen | |
| Nominaal meetniveau | Chi2 toets |
| Ordinaal meetniveau | Kruskal-Wallis test |
| Interval of ratio meetniveau | Variantie analyse (Anova) |
Het meetniveau
Het meetniveau is een onderwerp dat nog niet aan bod is gekomen. Toch is het meetniveau erg belangrijk om te kunnen bepalen welke statistische toets uitgevoerd kan worden. Er worden vier meetniveaus onderscheiden: nominaal, ordinaal, interval en ratio. Het laagste meetniveau is het nominale meetniveau. Dat betekent dat een bepaalde variabele twee of meer categorieën heeft die van elkaar verschillen. Zo kent bijvoorbeeld de variabele in figuur 6.2.1 drie categorieën: eigenaar-bewoner, huurder van een sociale huurwoning en huurder van een particuliere huurwoning. Het volgende meetniveau is het ordinale meetniveau. Een variabele met dit meetniveau heeft niet alleen minimaal twee verschillende categorieën, maar deze categorieën hebben ook een bepaalde rangordening, bijvoorbeeld van laag naar hoog of van “helemaal mee oneens” naar “helemaal mee eens”. De variabele die de tevredenheid met de woning aangeeft in het hiervoor genoemde voorbeeld kent een ordinaal meetniveau; in dit geval is er een oplopende schaal in tevredenheid van “zeer ontevreden” naar “zeer tevreden”. Het derde meetniveau is het interval meetniveau. Dit is een meetniveau dat in de praktijk maar zeer weinig voorkomt. Naast de verschillende categorieën en de rangordening is er de voorwaarde dat de onderlinge verschillen precies even groot zijn. Het meest bekende voorbeeld is de temperatuur in graden Celsius. Er zijn verschillende categorieën (elke graad is een categorie), er is een oplopende schaal (de temperatuur loopt van koud naar warm) en het verschil tussen bijvoorbeeld 8oC en 9oC (1 graad) is precies even groot als het verschil tussen 22oC en 23oC graden (1 graad). Wat echter ontbreekt bij het interval meetniveau is een natuurlijk nulpunt. Bij de temperatuur in graden Celsius is het nulpunt min of meer arbitrair gekozen. Hierdoor kunnen we bijvoorbeeld niet zeggen dat het vandaag (met een temperatuur van 20oC) twee keer zo warm is als gisteren, toen het 10oC was (bij twijfel, reken dit om naar graden Fahrenheit). Bij het vierde en hoogste meetniveau geldt dat er naast de vorige drie genoemde eisen ook sprake is van een natuurlijk nulpunt. We kunnen hierbij denken aan het aantal personen dat in een huis woont of het aantal vierkante meters dat de woonkamer beslaat. Nu kunnen we wel zeggen dat een woonkamer van 20 m2 twee keer zo groot als een woonkamer van 10 m2.
Ten slotte
Dit hoofdstuk heeft de handvatten aangereikt om met beschrijvende en toetsende statistiek aan de slag te gaan. De beschrijvende statistiek beperkt zich tot het beschrijven van resultaten op basis van de steekproef waarbij het onderzoek is uitgevoerd. De toetsende statistiek gebruikt de resultaten die zijn gevonden in de steekproef om uitspraken te doen over de populatie waaruit de steekproef geselecteerd is. Hierbij worden van tevoren hypothesen opgesteld en wordt de nulhypothese van “geen effect” op basis van de resultaten van de statistische toets al dan niet verworpen.
bRonnen
Baarda B, van Dijkum C, de Goede M (2014). Basisboek statistiek met SPSS. Noordhoff Uitgevers BV
CBS (2019). Huurders minder tevreden met woning. Geraadpleegd op 6 juli 2020 van: https://www.cbs.nl/nl-nl/nieuws/2019/38/huurders-minder-tevreden-met-woning
Field A (2017). Discovering statistics using IBM SPSS statistics (5th ed). Sage Publications Ltd
Saunders M, Lewis P, Thornhill E (2019). Methoden en technieken van onderzoek (8e druk). Pearson Benelux BV
NOS (2020). Waarom blijven de huizenprijzen stijgen, ondanks de Corona crisis? Geraadpleegd op 6 juli 2020 van: https://nos.nl/artikel/2338136-waarom-blijven-de-huizenprijzen-stijgen-ondanks-de-coronacrisis.html
