3
Dr. Kevin Bracker; Dr. Fang Lin; and jpursley
Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.
– Albert Einstein
Chapter Learning Objectives
After completing this chapter, students should be able to
- Explain the concepts of future value, present value, annuities, and discount rates
- Solve for the future value, present value, payment, interest rate or number of periods using the 5-key approach on a financial calculator
- Work with annual, semi-annual, quarterly, monthly, biweekly, weekly, or daily periods
- Solve for the present value of a perpetuity
- Solve for the present value or future value of an uneven cash flow stream
- Solve for the interest rate implied by an uneven cash flow stream
- Explain, calculate, and compare investments based on the effective annual rate
- Perform complex time value of money calculations (problems where multiple steps are required in order to reach the final solution)
The Power of Compound Interest
The quote at the start of the chapter is often attributed to Albert Einstein (despite some controversy as to the accuracy of that attribution). However, the validity of the statement itself has merit. Positive returns on investments over long periods of time are central to making money work for you as the power of compounding allows for geometric growth. Consider the following table (before long, you’ll be able to verify these calculations) of someone saving $250 per month for various times at various rates of return. Note that an individual who is 25 would have about 40 years until a standard retirement at age 65 and, assuming their employer offers a 50% match on retirement savings plans such as a 401(k), a total contribution of $250 each month would only be $2000 per year out of pocket before taxes.
Table: Future Value of $250 per month investment
| Years/Rate of Return | 5% | 10% | 15% |
| 1 | $3,069.71 | $3,141.39 | $3,215.09 |
| 5 | $17,001.52 | $19,359.27 | $22,143.63 |
| 10 | $38,820.57 | $51,211.24 | $68,804.26 |
| 15 | $66,822.24 | $103,617.59 | $167,126.69 |
| 20 | $102,758.42 | $189,842.21 | $374,309.87 |
| 25 | $148,877.43 | $331,708.35 | $810,882.40 |
| 30 | $208,064.66 | $565,121.98 | $1,730,819.90 |
| 35 | $284,023.11 | $949,159.51 | $3,669,295.04 |
| 40 | $381,505.04 | $1,581,019.90 | $7,754,013.69 |
| 45 | $506,609.32 | $2,620,625.43 | $16,361,256.65 |
| 50 | $667,162.99 | $4,331,097.70 | $34,498,278.44 |
Take a moment to review the table above. Note that at 5 years out, the rate of return makes some difference, but not a dramatic difference. By 15 years out, an individual would have 2.5 times as much at the 15% rate of return as the 5% rate of return. By 30 years out, the 10% rate of return is 2.7 times as much as the 5% rate of return and the 15% rate of return has accumulated 8.3 times the wealth. By 40 years out, an individual has invested $120,000 into her retirement savings (40 years at $3000 per year – with the potential for some of that $120,000 coming from the employer). The power of compounding has generated about $261,500 at 5%, nearly $1.5 million at 10%, and over $7.5 million at 15%. This example illustrates how powerful time and return are as tools for building wealth. Now it is time to show you how to do these and other time value of money calculations.
Future Value
When you put your money in a savings account (or invest it in some fashion), you earn a certain return (sometimes called interest) in order to compensate you. Because of this, a dollar today is not worth the same amount as a dollar sometime in the future. Since you earn money on the dollar invested (or saved) today, you will have more than a dollar at some later future point (making a dollar today worth more than the same dollar received later). The specific amount that you will have at the future date is referred to as a Future Value.
Consider if you had $100 today and were able to earn 12% per year by putting that money in a savings account at XYZ bank. How much would you have in one year? Two years? Three years? At first, you might think that you would have $112 in one year, $124 in two years and $136 in three years as you would earn $12 per year in interest. However, this is WRONG! It ignores the concept of compounding. After one year, you would indeed have $112. However, during the second year you earn 12% interest on the full $112 instead of only the $100 you started with. Therefore, you will earn $13.44 (=112×0.12) in interest in the second year and have $125.44 in two years. During the third year, you will earn $15.05 (=125.44×0.12) in interest and have $140.49 in three years. Therefore, the Future Value of $100 for three years at 12% is $140.49. In other words, $100 today is equivalent to $140.49 received three years from now assuming that you can earn 12% interest annually.
Solving for Future Value
We have three ways to solve for the FV: formula, financial table, and financial calculator.
Method 1: Using a Formula to Find the FV
The first is directly with a formula. Under this method, we use the following formula:
[latex]FV=PV(1+k)^n[/latex]
where
FV is the future value (in year n) for which we are trying to solve
PV is the present value (how much we have today)
k is the rate of return we are earning (also referred to as the interest rate, required return, growth rate, or discount rate)
n is the number of years which we will be saving (or investing) the money.
Method 2: Using a Table to Find the FV
The second method is to use Financial Tables, in Appendix A. Financial tables are cumbersome and don’t allow us as much flexibility as other methods, so they will not be covered in this text.
Method 3: Using a Financial Calculator to Find the FV
The third method (and the method focused on here) is to use the financial calculator or spreadsheet. Each financial calculator follows the same basic ideas, but the specifics are different for each brand of calculator. The steps below are for the HP10BII, TI-BAII+ and TI-83/84. If this is the first time using your financial calculator, see the detailed instructions Setting up Your Financial Calculator, in Appendix B. Please pause here to read that and set up your financial calculator before proceeding.
Calculator Steps to Compute FV:
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: Enter N Step 2: Enter I/YR Step 3: Enter 0 for PMT Step 4: Enter PV Step 5: Press the FV key |
Step 1: Enter N Step 2: Enter I/YR Step 3: Enter 0 for PMT Step 4: Enter PV Step 5: Press the CPT key Step 6: Press the FV key |
Go to APPS⇒Finance⇒ TVM_Solver Step 1: Enter N Step 2: Enter I/YR Step 3: Enter 0 for PMT Step 4: Enter PV Step 5: Move to FV line and press the ALPHA SOLVE key |
Note: The order of steps 1-4 is not important. The FV answer will appear as a negative number, ignore the negative sign for now. For the TI-83/84 calculators your P/Y and C/Y on the onscreen display should both be 1 for now.
Example: Finding FV using the Financial Calculator
Find the Future Value of $350 invested for 25 years at 9.5% per year.
Step 1: 25 N
Step 2: 9.5 I/YR
Step 3: 350 PV
Step 4: 0 PMT
Step 5: FV⇒
You should get a solution of $3383.93.
In other words, if we invest $350 today and let it compound at 9.5% per year for 25 years, we will have $3383.93 at the end of the 25th year.
Technically, you will get a value of -3383.93. The negative sign is an important aspect of financial calculators. The calculator is looking for the solution that balances both parties of a transaction. Here, since the $350 starting value was positive, the calculator assumes that this amount is being received today. If an individual receives $350, that individual needs to pay back $3383.93. Positive values represent cash inflows and negative values represent cash outflows. In a problem like this, it is not essential. However, later in the chapter, we will introduce problems where the cash flow direction is essential. Specifically, whenever there are nonzero values for two or three of the cash flows (PV, PMT, and/or FV), cash flow direction matters. In those cases, figure out if the cash flow is coming to you (available at that moment to spend) or the cash flow is going away from you (set aside into a savings plan). If the cash flow is coming to you, it is positive. If it is going away from you, it is negative. If we applied that logic in this example, the $350 PV would actually be -350. However, this would not change the value of the FV other than to make it positive.
Present Value
The flip side of Future Value is Present Value. Future value tells us how much a certain amount of money will be worth at some future date assuming a certain rate of return. However, what if we know how much we are supposed to get at some point in the future and want to know what it is worth to us today? Now we must find the Present Value. Assume we are offered an opportunity to receive $200 at the end of two years (call it investment A). How much is this opportunity worth to us today assuming we could earn 8% by placing our money in a savings account (that has risk similar to investment A)? To answer this, we must ask how much we would need to place in a savings account today in order to have $200 at the end of the two years.
[latex]FV=PV(1+k)^n[/latex]
[latex]200=PV(1.08)^2[/latex]
[latex]\frac{200}{(1.08)^2}=PV[/latex]
[latex]\$171.47=PV[/latex]
If we had $171.47 today and placed it in a savings account earning 8%, we would have $200 in two years (the same as through investment A). Assuming that investment A had the same degree of risk as our savings account, then we would buy investment A if it was available for less than $171.47 and put our money in the savings account if investment A cost more than $171.47. We could say that the present value of investment A is $171.47.
Solving for Present Value
We have three ways to solve for the PV: formula, financial table, and financial calculator.
Method 1: Using a Formula to Find the PV
The first is directly with a formula. Under this method, we use the following formula:
[latex]PV=\frac{FV}{(1+k)^n}[/latex]
where
FV is the future value (in year n) that we plan to receive
PV is the present value (how much it is worth to us today)
k is the rate of return we can earn elsewhere (also referred to as the compound rate, required return, or discount rate)
n is the number of years which we will have to wait before receiving the money.
Method 2: Using a Table to Find the PV
The second method is to use financial tables and will not be covered in this text.
Method 3: Using a Financial Calculator to Find the PV
The third method is to use the financial calculator (or spreadsheet). Each financial calculator follows the same basic ideas, but the specifics are different for each brand of calculator. The steps below are for the HP10BII, TI-BAII+ and TI-83/84.
Calculator Steps to Compute PV
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: Enter N Step 2: Enter I/YR Step 3: Enter 0 for PMT Step 4: Enter FV Step 5: Press the PV key |
Step 1: Enter N Step 2: Enter I/YR Step 3: Enter 0 for PMT Step 4: Enter FV Step 5: Press the CPT key Step 6: Press the PV key |
Go to APPS⇒Finance⇒ TVM_Solver Step 1: Enter N Step 2: Enter I/YR Step 3: Enter 0 for PMT Step 4: Enter FV Step 5: Move to PV line and press the ALPHA SOLVE key |
Note: The order of steps 1-4 is not important. The PV answer will appear as a negative number, ignore the negative sign for now.
Example: Finding PV using the Financial Calculator
Find the Present Value of $5000 received 15 years from today with a 9.5% discount rate.
Step 1: 15 N
Step 2: 9.5 I/YR
Step 3: 0 PMT
Step 4: 5000 FV
Step 5: PV⇒
You should get a solution of $1281.62
In other words, if we are offered the opportunity to receive $5000 at the end of 15 years that is equivalent to receiving $1281.62 today.
Annuities
The examples previously discussed are for situations where we have a specific amount today and want to know what it is worth at some point in the future (FV) or when we plan to receive a certain amount at some point in the future and want to know what it is worth today (PV). These are referred to as lump sum situations because there is only one cash flow that we are discounting or compounding.
 An annuity is different in that with an annuity we have the same exact amount being received (or paid) at the end of each period over a number of periods. For example, if we win the lottery that is usually paid in equal installments over a twenty-five year period. A $1,000,000 jackpot would be paid at $40,000 per year for twenty-five years. This is said to be an annuity. (Technically the lottery is an “annuity due” because the first payment is paid today, or the beginning of the period, as opposed to the end of the period).
An annuity is different in that with an annuity we have the same exact amount being received (or paid) at the end of each period over a number of periods. For example, if we win the lottery that is usually paid in equal installments over a twenty-five year period. A $1,000,000 jackpot would be paid at $40,000 per year for twenty-five years. This is said to be an annuity. (Technically the lottery is an “annuity due” because the first payment is paid today, or the beginning of the period, as opposed to the end of the period).
Timelines: Let us pause here for a moment to introduce an important tool used in time value of money – timelines. Timelines provide an aid that helps us better visualize what the cash flow stream looks like. Consider an annuity that pays $2000 per year for 4 years with an 8% discount rate. We can illustrate this on a timeline as follows:
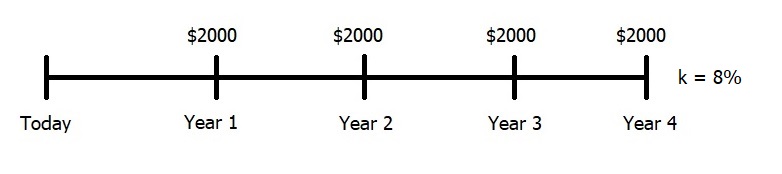
Note that the hashmarks represent the end of the time increment and the space between the hashmarks represent the time increment itself. In other words, the year 1 hashmark represents the end of year 1 where the annuity makes its first $2000 payment. Some students find timelines very helpful and use them for most time value of money problems while others use them less frequently. However, when we get to the section on complex time value of money problems later in this chapter, most students will find timelines quite beneficial.
Solving for Present Value of an Annuity
We have three ways to solve for the PV of an annuity: formula, financial table, and financial calculator.
Method 1: Using a Formula to Find the PV of an Annuity
The first is directly with a formula. Under this method, we use the following formula:
[latex]PVA=PMT\Big(\frac{1-\frac{1}{(1+k)^n}}{k}\Big)[/latex]
where
PVA is the present value of the anticipated cash flow stream (annuity)
PMT is the annuity payment (how much we receive or save each period)
k is the rate of return we can earn elsewhere (also referred to as the compound rate, required return, or discount rate)
n is the number of periods which we will have to wait before receiving the money.
Method 2: Using a Table to Find the PV of an Annuity
The second method is to use financial tables and will not be covered in this text.
Method 3: Using a Financial Calculator to Find the PV of an Annuity
The third method is to use the financial calculator (or spreadsheet) which is what we will focus on. Let’s walk through an example with the financial calculator. An investment that pays $100 at the end of each year for 4 years is an annuity (note that a clue for annuities is to look for the word “each’ or “every” to indicate that the same cash flow is being repeated multiple times). If we wanted to know what that investment is worth to us today and we had a 10% discount rate, we would be finding the present value of that annuity.
Calculator Steps to Compute PV of an Annuity
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: 4 N Step 2: 10 I/YR Step 3: 100 PMT Step 4: 0 FV Step 5: PV⇒ |
Step 1: 4 N Step 2: 10 I/YR Step 3: 100 PMT Step 4: 0 FV Step 5: Press the CPT key Step 6: Press the PV key |
Go to APPS⇒Finance⇒ TVM_Solver Step 1: 4 N Step 2: 10 I/YR Step 3: 100 PMT Step 4: 0 FV Step 5: Move to PV line and press the ALPHA SOLVE key |
Note: The order of steps 1-4 is not important. The PV answer will appear as a negative number, ignore the negative sign for now.
You should get a solution of $316.99
Solving for Future Value of an Annuity
As with the other TVM calculations we have encountered, there are 3 basic methods to solve for the FV of an annuity: formula, financial table, and financial calculator.
Method 1: Using a Formula to Find the FV of an Annuity
The first is directly with a formula. Under this method, we use the following formula:
[latex]FVA=PMT\Big(\frac{(1+k)^n-1}{k}\Big)[/latex]
where
FVA is the future value that our cash flow stream will grow to at the end of n periods
PMT is the annuity payment (how much we receive or save each period)
k is the rate of return we can earn elsewhere (also referred to as the compound rate, required return, or discount rate)
n is the number of periods which we will have to wait before receiving the money.
Method 2: Using a Table to Find the FV of an Annuity
The second method is to use financial tables. These tables are included in Appendix A and will not be covered in this text.
Method 3: Using a Financial Calculator to Find the FV of an Annuity
The third method is the financial calculator (or spreadsheet) approach. Let’s walk through an example using the financial calculator to solve for the future value of an annuity. We want to save $1000 per year (at the end of each year) for 10 years at 12%. How much will this be worth at the end of the 10th year?
Calculator Steps to Compute FV of an Annuity
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: 10 N Step 2: 12 I/YR Step 3: 1000 PMT Step 4: 0 PV Step 5: FV |
Step 1: 10 N Step 2: 12 I/YR Step 3: 1000 PMT Step 4: 0 PV Step 5: Press the CPT key Step 6: Press the FV key |
Go to APPS⇒Finance⇒ TVM_Solver Step 1: 10 N Step 2: 12 I/YR Step 3: 1000 PMT Step 4: 0 PV Step 5: Move to FV line and press the ALPHA SOLVE key |
Note: The order of steps 1-4 is not important. The FV answer will appear as a negative number, ignore the negative sign for now.
You should get a solution of $17,548.74
Note: Ordinary annuities (both present value and future value) assume that cash flows will arrive at the end of each period. Occasionally, you might encounter an annuity due (which means that cash flows arrive at the BEGINNING of each period). It is easy to adjust for this when using a financial calculator by changing the calculator from END of period cash flows to BEGINNING of period cash flows. This process is described in Setting up Your Financial Calculator in Appendix B (for the TI-83/84, it is just part of the onscreen display in the TVM_Solver).
Solving for PMT, I/YR, or N
Sometimes you may need to find something other than the present value or future value. For instance, you may want to know how much you have to save per year to reach a certain future value (or how much you must earn as a rate of return or how many years it will take). If you are using a financial calculator, these are relatively easy. For example, assume you have $2000 saved already and want to save another $5000 per year to accumulate $80,000 after 10 years. What rate of return must you earn?
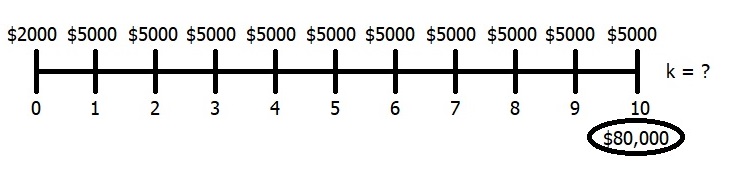
Calculator Steps for the Solution
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: 10 N Step 2: 80000 FV Step 3: -5000 PMT Step 4: -2000 PV Step 5: I/YR |
Step 1: 10 N Step 2: 80000 FV Step 3: -5000 PMT Step 4: -2000 PV Step 5: Press the CPT key Step 6: Press the I/YR key |
Go to APPS⇒Finance⇒ TVM_Solver Step 1: 10 N Step 2: 80000 FV Step 3: -5000 PMT Step 4: -2000 PV Step 5: Move to I% line and press the ALPHA SOLVE key |
Solution = 8.83%
Reminder: Either the PMT must be negative and the FV positive or the PMT positive and the FV negative. It doesn’t matter which way you do it, but one must be negative and the other positive.
Solving for N and PMT is done along similar lines.
Perpetuities
A Perpetuity is an annuity that lasts forever. While it is difficult to imagine a situation where an individual could buy a cash flow stream that will pay a fixed amount per year through infinity, perpetuities can be useful tools when dealing with long, constant cash flow streams. Consider someone wanting to fund a scholarship or plan for retirement where she is not sure how long she’ll live. A perpetuity can provide a reasonable approximation in either of those situations.
How much would a perpetuity of $100 be worth assuming a discount rate of 10%? Remember this is $100 per year forever. It would seem that this would be worth an infinite amount. However, consider what would happen if you had $1000 today and could put it in the bank to earn 10% interest. You would receive $100 per year and never touch the principal. You would essentially be buying a $100 perpetuity (assuming the bank didn’t change the interest rate). Therefore, a perpetuity has a finite value. The formula for finding the present value of a perpetuity is as follows:
[latex]PV=\frac{PMT}{k}[/latex]
Note: When using this formula, always plug in k as a decimal so that 10% is 0.10
Uneven Cash Flow Streams
Sometimes you will encounter a situation where you have more than one payment, but it is not the same each year. Remember that an annuity requires the payment to be the same each year. If you have multiple cash flows, but they are not the same, you have an uneven cash flow stream. In order to solve a problem like this, treat it as a series of single cash flows (or possibly a series of smaller annuities).
Net Present Value of an Uneven Cash Flow Stream
Consider the following example: you have an investment project that will pay the following cash flows:
Year 1 $1000
Year 2 $500
Year 3 $2000
Year 4 $2000
The discount rate is 15%. Find the Present Value.
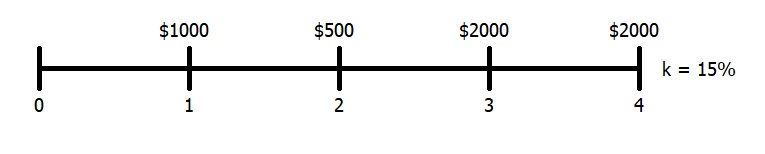
Calculator Steps to Compute PV of an Uneven Cash Flow Stream
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: Clear All Step 2: 0 CFj Step 3: 1000 CFj Step 4: 500 CFj Step 5: 2000 CFj Step 6: 2 Nj Step 7: 15 I/YR Step 8: NPV |
Step 1: CF CLR Work Step 2: 0 Enter ↓ Step 3: 1000 Enter ↓↓ Step 4: 500 Enter ↓↓ Step 5: 2000 Enter ↓ Step 6: 2 Enter Step 7: NPV 15 Enter ↓ Step 8: CPT |
Go to APPS⇒Finance⇒ Step 1: Select npv( Step 2: Enter the given information in the following format: npv(InterestRate, CF0, {CF Stream}, {CF Frequencies} npv(15,0,{1000,500,2000},{1,1,2} Step 3: Press the SOLVE key |
Solution $3706.18
Note for HP10BII+: The Nj key is used to tell the calculator the number of times that the same cash flow will be received consecutively. If the cash flow only occurs once (in a row) then we do not need to use the Nj key. However, when we have the same cash flow multiple times in a row (such as the $2000 for two years), we can use the Nj key to tell the calculator that this $2000 will occur in two consecutive years.
Note for TI-BAII+: The F screen that appears after you enter a cash flow and down arrow is used to tell the calculator the number of times we have that same cash flow consecutively. If the cash flow only occurs once (in a row) then we do not F screen and just down arrow past it. However, when we have the same cash flow multiple times in a row (such as the 2000 for two years), we use the F screen to tell this to the calculator. The calculator does not have a F screen after the initial cash flow, so we do not need the double down arrow after entering the initial CF.
The above calculator methods are referred to as your Cash Flow Register or Cash Flow Worksheet. It is essential that you always clear all/clear work before entering any cash flows. If you do not do this you will be adding cash flows to a previous problem instead of starting a new problem. The TI-83/84 does not utilize this type of register and does not need to be cleared.
Future Value of an Uneven Cash Flow Stream
The NPV function gives you the present value. You may alternatively want to know how much you will have at the END of the time period (solve for the future value). If this is the case, you start by solving for the NPV. Once you have that, use the 5-key approach to bring that present value forward to the end of the time horizon. For example, if we wanted to know what the above cash flow stream was worth at the END of the fourth year, we would start by solving for the NPV and get the same $3706.18 we calculated earlier. Then, we would go to our 5-key and solve for the future value as follows:
Step 1: 4 N
Step 2: 15 I/YR
Step 3: 3706.18 PV
Step 4: 0 PMT
Step 5: Solve for FV⇒$6482.13
When calculating the PV of an uneven cash flow stream, it should always be less than the sum of the cash flows. When calculating the FV of an uneven cash flow stream, it should always be more than the sum of the cash flows. Also, many financial calculators allow you to solve directly for the future value of an uneven cash flow stream. To see if yours does this, consult your user manual or ask your instructor.
Finding the discount rate of an Uneven Cash Flow Stream
We can also find the discount rate (I/Y) if we have uneven cash flows. Consider the following example: We have an investment project that will pay the following cash flows:
Year 1 $1000
Year 2 $500
Year 3 $2000
If the present value of this investment is $3000, what is the discount rate?
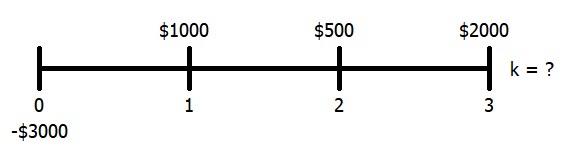
Calculator Steps to Compute I/Y of an Uneven Cash Flow Stream
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: Clear All Step 2: -3000 CFj Step 3: 1000 CFj Step 4: 500 CFj Step 5: 2000 CFj Step 6: IRR/YR⇒ |
Step 1: CF CLR Work Step 2: -3000 Enter ↓ Step 3: 1000 Enter ↓↓ Step 4: 500 Enter ↓↓ Step 5: 2000 Enter Step 6: IRR Step 7: CPT |
Go to APPS⇒Finance⇒ Step 1: Select irr( |
Solution 7.06%
Note for HP10BII+: The IRR/YR is not the same key as you used for the I/YR, but it serves a similar role — finding the discount rate (or rate of return) for a cash flow stream. The difference is that they I/YR key only works with single cash flows or annuities while the IRR/YR key works with uneven cash flows.
Note for TI-BAII+: The IRR is not the same key as you used for the I/Y, but it serves a similar role — finding the discount rate (or rate of return) for a cash flow stream. The difference is that the I/Y key only works with single cash flows or annuities while the IRR key works with uneven cash flows.
CF0 will always be negative when calculating IRR. If you end up with an error message when calculating the IRR, one of the first things you should do is make sure that your CF0 was a negative value.
Non-Annual Compounding
The more frequently interest is compounded, the greater the effective yield on our savings. Many banks use non-annual compounding periods (monthly, daily, etc). In order to make comparisons, we must find the effective annual yield. This tells us how much we are earning on an annual basis.
Using a Formula to Find the Effective Annual Yield
The formula for effective annual yield is as follows:
[latex]k_{eff}=\Big(1+\frac{k_{nom}}{m}\Big)^m-1[/latex]
where
keff is the effective annual yield
knom is the nominal or stated yield
m is the number of compounding periods per year
For example, what is the effective interest rate of 8% compounded daily?
[latex]k_{eff}=\Big(1+\frac{0.08}{365}\Big)^{365}-1[/latex]
Note: Be careful not to round when you take .08/365 or you will end up with significant error after compounding it 365 times.
Using a Calculator to Find the Effective Annual Yield
As an alternative, you could use your financial calculator to find the effective interest rate. Again, using 8% compounded daily.
Calculator Steps to Find the Effective Annual Yield
| HP10BII | TI-BAII+ | TI-83/84 |
| Step 1: 365 SHIFT P/YR Step 2: 8 SHIFT NOM% Step 3: SHIFT EFF% |
Step 1: 2nd I Conv I Conv is the shift of the 2 key Step 2: 8 Enter ↓↓ Step 3: 365 Enter ↑ Step 4: Press the CPT key |
Go to APPS⇒Finance⇒ Step 1: Select EFF( Step 2: Enter the given information in the following format: EFF(NOMINAL RATE,COMPOUNDING PERIODS PER YEAR) EFF(8,365) Step 3: Press SOLVE |
Solution 8.33%.
Note for HP-10BII+: You have changed your payments per year when doing this calculation. If you go back to another TVM problem, be sure to reset your payments per year to one.
Example: Solve a Problem Involving Non-Annual Compounding
We could also look at non-annual compounding with loans or investments. For example, consider a mortgage loan. You are borrowing $80,000 at an 8% rate with monthly payments for 30 years (note that non-annual annuities and lump sums work best with calculators), what is your monthly payment?
Step 1: Convert your calculator to monthly payments by entering 12 P/YR
Step 2: -80000 PV
Step 3: 8 I/YR
Step 4: 360 N (30 years at 12 months per year)
Step 5: 0 FV
Step 6: PMT
Solution = $587.01 per month
Be VERY careful if you change your payments per year to change it back to 1 P/YR when you are done. Also, each calculator is slightly different in how it sets the periods per year. Be sure to review the Setting up Your Financial Calculator in Appendix B for calculator specific instructions.
Return to Future Value Tables
Remember the table of future values that we used to start the chapter? We said that the value of $250 set aside every month for 40 years at 10% would be $1,581,019.90. We also suggested that by the end of this chapter, you would be able to do that calculation on your own. Well, now you can.
Step 1: Convert your calculator to monthly payments by entering 12 P/YR
Step 2: 0 PV
Step 3: 10 I/YR
Step 4: 480 N (40 years at 12 months per year)
Step 5: 250 PMT
Step 6: FV
Solution = $1,581,019.90
Complex Time Value of Money Problems
Everything above this point completes your “Time Value of Money Toolbox.” All the examples to this point have been straight-forward situations. However, sometimes we have what we refer to as complex time value of money problems where there are multiple issues that need addressed within one problem. One of the most common examples of this would be a retirement problem where you have X dollars available today, want to be able to withdraw a certain cash flow stream at retirement throughout your retirement years and want to find out how much you need to save each month until retirement between now and the day you retire to achieve your goal. In order to solve a problem like this, you need to visualize (a time line is very helpful) what information you have and what you are missing (that you need to solve for). You will often need to break this down into multiple steps.
Example: Solve a Complex Time Value of Money Problem
Consider a situation where you are saving for retirement. You currently have $40,000 saved and would like to save an additional $75 per week for the next 30 years. You estimate that when you retire (30 years from today), you want to be able to withdraw $750 each week for the next 20 years and have $200,000 left over at the end of the 20-year retirement period. Assuming you earn 5% during retirement, what rate of return must you earn during the next 30 years to meet your goal?
One way to approach this is to start with a timeline. Note that each period is one week and there are 52 weeks per year. This means that we will have 1560 periods until retirement (1560 = 30×52) and another 1040 periods until the end of retirement (1040 = 20×52). This provides a total of 2600 periods for the entire 50 year time (2600 = 1560 + 1040). Once we’ve created the timeline, we can split it into two timelines. Timeline one will begin today and go to retirement (period 1560) and timeline 2 will begin at retirement (also period 1560) and go to the end of the retirement time frame (period 2600). Here, the timelines help us visualize the information that we know and what we need to find out (specifically our rate of return we must earn over the first 30 years).
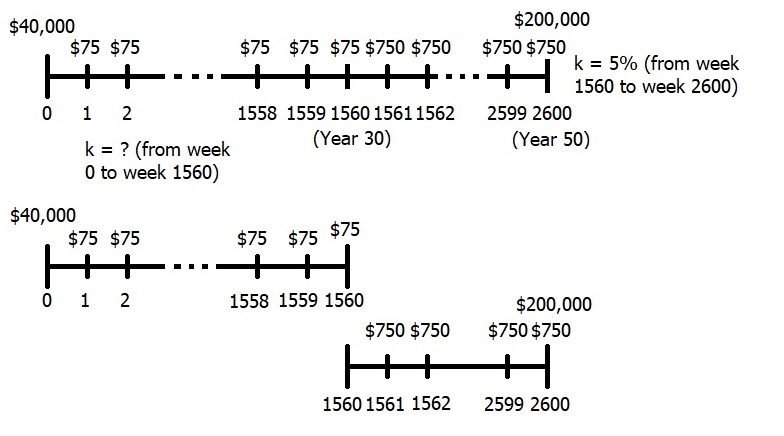
Now we can start the calculations. To start, you need to figure out how much you will require at the end of the 30 years. This is the amount you want to have when you retire.
Step 1: Solve for how much you need at retirement.
Set your calculator to 52 periods per year to reflect weekly withdraws during retirement
Set your N to 1040 (52 periods per year for 20 years = 1040 weekly periods)
Set your PMT to 750 (to reflect the weekly withdraw)
Set your FV to 200,000 (to reflect the amount left over)
Set your I/YR to 5 (for your rate of return during retirement)
Solve for PV ⇒$566,527.38
Note – your PMT and FV need to be the same sign. You can make them both positive or both negative, but they are both flowing in the same direction so must be the same sign.
Step 2: Now that you know how much you need when you retire ($566,527.38), you can calculate what rate of return you need to earn over the next 30 years to get there.
Keep your calculator set to 52 periods per year as you are making weekly contributions
Set your N to 1560 (52 periods per year for 30 years = 1560 weekly periods)
Set your PV to -40,000 (to reflect the initial $40,000 contribution)
Set your PMT to -75 (to reflect your weekly $75 contribution)
Set your FV to 566,527.38 (to reflect how much you need at retirement)
Solve for I/YR ⇒5.98%
Note – your PV and PMT both need to be the same sign. Again, you can make them positive or negative, but they are both flowing in the same direction. The FV needs to be the opposite sign. The easiest way to think of this is that you are giving up the $40,000 today and the $75 per week in order to get back the $566,527.38 30 years from today.
Key Takeaways
Time value of money is one of the most powerful and most important concepts in finance. It essentially is as simple as recognizing that because we can earn a return on our money, the value of money changes depending on when it is received or spent. One dollar today is worth more than one dollar received next year. The value of the dollar initially is referred to as a present value while the value of the dollar at a later point in time is referred to as the future value. Compound interest implies that money will grow exponentially over time instead of linearly. This means that relatively small increases in rates of return or time horizons have more power to increase wealth. After completing this chapter, you should be comfortable performing many calculations to see exactly how time value of money can work for you.
Exercises
Question 1
Explain why $1 received today is worth more than $1 received one year from today.
Question 2
What do we mean when we refer to an annuity? How is an annuity different from an annuity due?
Question 3
What is the relationship between present value and future value?
Question 4
How do we determine the appropriate discount rate to use when finding present value?
Question 5
Why is compounding on a monthly basis better for us than compounding on an annual basis?
Problem 1
Determine the answer to each of the following questions.
1a. Find the Future Value of $2500 invested today at 11% for 10 years.
1b. Find the Future Value of $2500 invested today at 11% for 30 years.
1c. Find the Present Value of $6000 received 10 years from today if the discount rate is 5%.
1d. Find the Present Value of $6000 received 10 years from today if the discount rate is 10%.
1e. Find the Future Value of $3000 per year (at the end of each year) invested at 6% for 30 years.
1f. Find the Future Value of $3000 per year (at the end of each year) invested at 12% for 30 years.
1g. Find the Present Value of $4000 per year (at the end of each year) if the discount rate is 15% for 20 years.
1h. Find the Present Value of $4000 per year (at the end of each year) if the discount rate is 15% for 40 years.
Problem 2
Find the interest rates implied by each of the following:
2a. You borrow $1500 today and promise to repay the loan by making a single payment of $2114.00 in 5 years.
2b. You invest $500 today and receive a promise of receiving back $193.50 for each of the next 4 years.
Problem 3
If $2000 is invested today at a 12% nominal interest rate, how much will it be worth in 15 years if interest is compounded
3a. Annually
3b. Quarterly
3c. Monthly
3d. Daily (365-days per year)
Problem 4
How long will it take your money to triple given the following interest rates?
4a. 5%
4b. 10%
4c. 15%
Problem 5
After graduating from college you make it big — all because of your success in business finance. You decide to endow a scholarship for needy finance students that will provide $5000 per year indefinitely, beginning 1 year from now. How much must be deposited today to fund the scholarship under the following conditions.
5a. The interest rate is 10%
5b. The interest rate is 10% and the first payment is made 6 years from today instead of 1 year from today.
Problem 6
Find the present value of the following cash flow stream if the discount rate is 12%:
Years 1-10 $4000 per year
Years 11-15 $6000 per year
Years 16-20 $8000 per year
Problem 7
Find the value of the following cash flow stream at the end of year 30 if the rate of return is 8.75%:
Years 1-5 $3000 per year
Year 6 $7500
Years 7-15 $9000 per year
Years 16-30 $12,000 per year
Problem 8
Find the effective annual rate of interest for a nominal rate of 9% compounded
8a. Annually
8b. Quarterly
8c. Monthly
8d. Daily (365 days per year)
Problem 9
Your firm has a retirement plan that matches all contributions on a one-to-two basis. That is, if you contribute $3000 per year, the company will add $1500 to make it $4500. The firm guarantees a 9% return on your investment. Alternatively, you can “do-it-yourself” and you think you can earn 12% on your money by doing it this way. The first contribution will be made 1 year from today. At that time, and every year thereafter, you will put $3000 into the retirement account. If you want to retire in 25 years, which way are you better off?
Problem 10
Jen is planning for retirement. She plans to work for 32 more years. She currently has $15,000 saved and, for the next 15 years, she can save $6,000 at the end of each year. Fifteen years from now, she wants to buy a weekend vacation home that she estimates will require her to withdraw $100,000. How much will she have to save in years 16 through 32 so that she has exactly $750,000 saved when she retires? Assume she can earn 9% throughout the 32-year period.
Problem 11
You are a recent college graduate and want to start saving for retirement. You plan to save $2000 per year for the next 15 years. After that you will stop contributing and just allow your savings to accumulate for another 20 years. Your twin brother would rather wait awhile before he starts saving. He is not going to put away anything for the next ten years, then he will start making contributions at the end of each year for the final 25 years. You both anticipate earning a 9.5% rate of return on your investments. How much must your brother put away at the end of each year to have the same amount of money for retirement as you?
Problem 12
You are considering purchasing a new home. The house you are looking at costs $120,000 and you plan to make a 10% down payment. You checked with a bank and they have two mortgage loan options for you. The first is a 15-year mortgage at 6.25%. The second is a 30-year mortgage at 6.50%.
12a. What are your monthly payments for each loan?
12b. What is the total you will pay over the life of the loan for each loan?
12c. After one year you get a job transfer and have to sell the house. What is the payoff value of your remaining loan balance (hint: find PV of remaining payments)?
12d. Over the first year, how much did you pay in principal and how much did you pay in interest?
Solutions to CH 3 Exercises
Student Resources
Table: Future Value of $250 per month investment, in Appendix B
Financial Tables, in Appendix A
Setting up Your Financial Calculator, in Appendix B
TVM 5-Key Approach Guided Tutorial with HP10BII+, in Appendix B
TVM 5-Key Approach Guided Tutorial with TI-BAII+, in Appendix B
TVM 5-Key Approach Guided Tutorial with TI-83 or TI-84, in Appendix B
Attributions
Image: Mixed from Godkänd Grön Handskrivning by Anthony Poynton is licensed under CC0 1.0
