附錄(一) 有效數字
定義
科學敘述中的有效數字,包含確定位數與 1 位不準確位數。例如以最小刻度為 mL 量筒量取液體,得到體積為 25.5 mL,則 25 為確定位數,最末一位 0.5 為不準確(估計)位數。
至於數字 0 是否為有效數字,則需視其位置而定,其規則如下:
-
位於有效數字中間之 0,為有效數字。例如: 30205(五位有效數字)、 1.009(四位有效數字)
-
位置在數值左邊的 0 不是有效數字。例如: 00123(三位有效數字)、0.026(二位有效數字)
-
位於小數點右邊,且為數值末端的 0,為有效數字。例如: 0.0550(三位有效數字), 10.00(四位有效數字)
-
整數末端之 0 可為有效數字或不是有效數字,例如 5000 無法確定有效位數,但表示為 5000. 則為四位有效數字,若以科學記號號表將更為清楚: 5.00×103(三位有效數字)、 5.000×103(四位有效數字)。
有效數字的運算
基本原則為僅保留一位不準確位數
-
加減
兩個以上數值的加減所得的和或差,其有效數字之定位應以位數最大者為主(如十位數大於個位數),其餘往右之數字均不能歸入有效數字。
如:
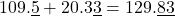 (底線表示不準確位數),因 109.5 中小數點後第一位已經是不準確位數,故計算結果應取 129.8,僅保留一位不準確位數。
(底線表示不準確位數),因 109.5 中小數點後第一位已經是不準確位數,故計算結果應取 129.8,僅保留一位不準確位數。 -
乘除
積或商應以有效數字位數最少的數值為主。
如:20.6 (三位) ÷ 1.5 (二位) × 1.009 (四位) ,其結果應記為 1.5×102,兩位有效數字
-
對數和反對數
通常將對數值化為真值後再進行運算。所取真值之有效位數應與原對數值之位數相同,但運算後之數值其有效位數可能會增加一位或減少一位。
如log(4.80×105)= log(4.80) + log(105),因指數與有效數字無關,上式應 = 0.681(三位)+ 5 = 5.681(四位)
-
在所有運算式子中,乘除因子(如1/2、√2、時間的換算)、常數(如π)之有效位數不作限制,亦不影響其他數值之運算結果。
有效數字的取捨
經過運算後的數值必須做適當的捨入,其規則為「四捨六入五成雙」而非「四捨五入」。
「五成雙」有下列三種狀況:
-
5 之後有非 0 數字則「入」,
如:10.55012 取三位有效數字時,其答案為 10.6。
-
5 之後沒有非 0 數字,5 前方為奇數則「入」,
如:23.7500 取三位有效數字時,其答案為 23.8
-
5 之後沒有非 0 數字,5 前方為偶數則「捨」,
如:0.234500 取三位有效數字時,其答案為 0.234
四、其他
由於有效數字是由量測的精確度所決定,當量測的工具越精確時,越能取得較多之有效位數,使用時亦須考慮可能的誤差。以普化實驗為例,誤差通常在 0.1 至數 %,有效位數如超過三位數是沒有必要的亦不合理的。
