35 Symmetrical and Non-traditional Scales
Symmetrical Scales
Symmetrical scales (sometimes called artificial scales) are created through an equal subdivision of the octave. The scale degrees are measured by half steps and whole steps. Symmetrical scales often use flexible enharmonic spelling.
It is easier to consider symmetrical scales in terms of the number of half steps between pitches, rather than the intervals.
| Interval | Number of half steps |
| m2 | 1 |
| M2 | 2 |
| m3 | 3 |
| P4 | 5 |
A. Chromatic Scale (1:1 model, with “1” indicating a half step)
The simplest symmetrical scale is the chromatic scale, which has 12 half steps.
B. Whole Tone Scale (2:2 model, with “2” indicating a whole step)
The whole tone scale equally subdivides the octave, resulting in a scale comprised of six whole steps.
There are only two possible whole tone scales, each a half step apart, either starting on C or C![]() /D
/D![]() . Whole tone scales starting on all other notes have the same collection of pitches as those on C or C
. Whole tone scales starting on all other notes have the same collection of pitches as those on C or C![]() /D
/D![]() . Enharmonic spelling is acceptable since there are no traditional harmonic relations associated with these scales.
. Enharmonic spelling is acceptable since there are no traditional harmonic relations associated with these scales.
The example below utilizes augmented triads based on a descending whole tone scale.
C. Octatonic Scale (2:1 or 1:2 model)
The scale can begin with the whole step (2:1 model) or half step (1:2 model). Both resulting scales subdivide the octave into eight steps.
The scale is sometimes called the diminished scale because it can be built from two diminished seventh chords a whole step apart (2:1 model) or two diminished seventh chords a half step apart (1:2 model).
To facilitate aural recognition, the 2:1 model can be perceived as two sets of four notes (tetrachords) from the minor scale (do – re – me – fa) a tritone apart.
The 1:2 model can be perceived as two minor tetrachords (t, – d – re – me) a tritone apart.
Since the octatonic scale lacks harmonic variety, composers often use the scale in a linear manner to create polyphonic compositions. One approach is to combine two tetrachords a tritone apart. The polytonal example below simultaneously implies both A minor and D-sharp minor.
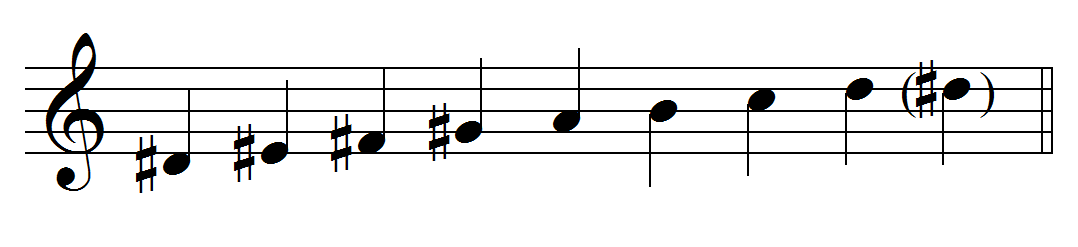
The octatonic scale also contains four 1:5 cells that alternate a half step and P4, which spans 5 half steps.
The example below utilizes the 1:5 compositional device along with mirror imitation.

D. 1:3 Scale
In addition to producing three minor triads and three major triads, augmented triads can be built on every note of the scale.
An example using the 3:1 scale in imitation, creating major and augmented chords.
Non-traditional Scales
Numerous artificial scales were utilized starting in the late 19th century. Two of the more commonly used artificial scales are the Lydian-Mixolydian and Hungarian minor/Arabic.
A. Lydian-Mixolydian (Overtone) Scale
The scale can be perceived as a Mixolydian scale with a Lydian element (A4) or a Lydian scale with a Mixolydian element (m7), or a major scale with an augmented fourth and a minor seventh.
The example below has a Lydian-Mixolydian flavor. The melody and ostinato of the first phrase is mirrored (inverted) in the second phrase. Tension is created in the final section by isolating smaller parts of the first two phrases using the fragmentation technique.
B. Hungarian Minor and Arabic Scales
Hungarian Minor
In addition to its use in folk songs, the scale was employed by composers including Chopin, Rimsky-Korsakov, Tchaikovsky, Scriabin, Bartók, and Kodály.
Examples of melodies using Hungarian minor:
Arabic Scale
The Arabic scale is a mode of the Hungarian minor scale from so to so (or mi to mi in la-minor). It is a variant of Phyrgian due to the cadential m2 between ra – do (or fa – mi in la-minor).
The final cadence in this Aeolian melody uses the descending Arabic scale.
Chromatic musicianship melodies #20 and #27 employ, at times, the Hungarian minor scale.
Practice
-
Write octatonic scales (both 1:2 and 2:1 models) starting on F, F
 , and G.
, and G. - Write Lydian-Mixolydian scales on D, E, F, G, and A. Use key signatures.
-
Write Hungarian minor scales on D, E, F, G, and A. Use key signatures.
-
Write Arabic scales on D, E, F, G, and A. Use key signatures.