Incidence matrix of a network
Mathematically speaking, a network is a graph of 
nodes connected by 
directed arcs. Here, we assume that arcs are ordered pairs, with at most one arc joining any two nodes; we also assume that there are no self-loops (arcs from a node to itself). We do not assume that the edges of the graph are weighted—they are all similar.
We can fully describe the network with the so-called arc-node incidence matrix, which is the 
matrix defined as
![\[ A_{ij} = \left\{ \begin{array}{ll} 1 & \text{if arc } j \text{ starts at node } i \\ -1 & \text{if arc } j \text{ ends at node } i \\ 0 & \text{otherwise.} \end{array} \right. , \quad 1 \le i \le m, \quad 1 \le j \le n. \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-789ad25e589ca5325a972bd07961f645_l3.png "Rendered by QuickLaTeX.com")
 |
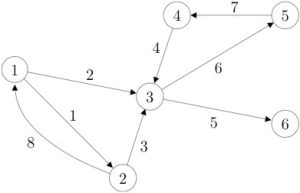The figure shows the graph associated with the arc-node incidence matrix
|
![\[ A = \left[ \begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\ \end{array} \right]. \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ecc6ac49b1215ac8e34b548c9e783d6a_l3.png "Rendered by QuickLaTeX.com")
See also: Network flow.
