30 POSITIVE SEMI-DEFINITE MATRICES
30.1. Definitions
For a given symmetric matrix ![]() , the associated quadratic form is the function
, the associated quadratic form is the function ![]() with values
with values
![]()
- A symmetric matrix
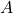 is said to be positive semi-definite (PSD, notation:
is said to be positive semi-definite (PSD, notation: 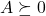 ) if and only if the associated quadratic form
) if and only if the associated quadratic form 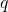 is non-negative everywhere:
is non-negative everywhere:
![]()
- It is said to be positive definite (PD, notation:
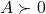 ) if the quadratic form is non-negative and definite, that is,
) if the quadratic form is non-negative and definite, that is, 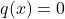 if and only if
if and only if 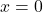 .
.
It turns out that a matrix is PSD if and only if the eigenvalues of ![]() are non-negative. Thus, we can check if a form is PSD by computing the eigenvalue decomposition of the underlying symmetric matrix.
are non-negative. Thus, we can check if a form is PSD by computing the eigenvalue decomposition of the underlying symmetric matrix.
Theorem: eigenvalues of PSD matrices
|
A quadratic form |
By definition, the PSD and PD properties are properties of the eigenvalues of the matrix only, not of the eigenvectors. Also, if the ![]() matrix
matrix ![]() is PSD, then for every matrix
is PSD, then for every matrix ![]() with
with ![]() columns, the matrix
columns, the matrix ![]() also is.
also is.
30.2. Special cases and examples
Symmetric dyads
Special cases of PSD matrices include symmetric dyads. Indeed, if ![]() for some vector
for some vector ![]() , then for every
, then for every ![]() :
:
![]()
More generally if ![]() , then
, then ![]() is PSD, since
is PSD, since
![]()
Diagonal matrices
A diagonal matrix is PSD (resp. PD) if and only if all of its (diagonal) elements are non-negative (resp. positive).
Examples of PSD matrices
30.3. Square root and Cholesky decomposition
For PD matrices, we can generalize the notion of the ordinary square root of a non-negative number. Indeed, if ![]() is PSD, there exists a unique PSD matrix, denoted
is PSD, there exists a unique PSD matrix, denoted ![]() , such that
, such that ![]() . We can express this matrix square root in terms of the SED of
. We can express this matrix square root in terms of the SED of ![]() , as
, as ![]() , where
, where ![]() is obtained from
is obtained from ![]() by taking the square root of its diagonal elements. If
by taking the square root of its diagonal elements. If ![]() is PD, then so is its square root.
is PD, then so is its square root.
Any PSD matrix can be written as a product ![]() for an appropriate matrix
for an appropriate matrix ![]() . The decomposition is not unique, and
. The decomposition is not unique, and ![]() is only a possible choice (the only PSD one). Another choice, in terms of the SED of
is only a possible choice (the only PSD one). Another choice, in terms of the SED of ![]() , is
, is ![]() . If
. If ![]() is positive-definite, then we can choose
is positive-definite, then we can choose ![]() to be lower triangular, and invertible. The decomposition is then known as the Cholesky decomposition of
to be lower triangular, and invertible. The decomposition is then known as the Cholesky decomposition of ![]() .
.
30.4. Ellipsoids
There is a strong correspondence between ellipsoids and PSD matrices.
Definition
We define an ellipsoid to be an affine transformation of the unit ball for the Euclidean norm:
![]()
where ![]() is an arbitrary non-singular matrix. We can express the ellipsoid as
is an arbitrary non-singular matrix. We can express the ellipsoid as
![]()
where ![]() is PD.
is PD.
Geometric interpretation via SED
We can interpret the eigenvectors and associated eigenvalues of ![]() in terms of the geometrical properties of the ellipsoid, as follows. Consider the SED of
in terms of the geometrical properties of the ellipsoid, as follows. Consider the SED of ![]() :
: ![]() , with
, with ![]() and
and ![]() diagonal, with diagonal elements positive. The SED of its inverse is
diagonal, with diagonal elements positive. The SED of its inverse is ![]() . Let
. Let ![]() . We can express the condition
. We can express the condition ![]() as
as
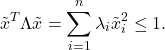
Now set ![]() ,
, ![]() . The above can be written as
. The above can be written as ![]() : in
: in ![]() -space, the ellipsoid is simply a unit ball. In
-space, the ellipsoid is simply a unit ball. In ![]() -space, the ellipsoid corresponds to scaling each
-space, the ellipsoid corresponds to scaling each ![]() -axis by the square roots of the eigenvalues. The ellipsoid has principal axes parallel to the coordinate axes in
-axis by the square roots of the eigenvalues. The ellipsoid has principal axes parallel to the coordinate axes in ![]() -space. We then apply a rotation and a translation to get the ellipsoid in the original
-space. We then apply a rotation and a translation to get the ellipsoid in the original ![]() -space. The rotation is determined by the eigenvectors of
-space. The rotation is determined by the eigenvectors of ![]() , which are contained in the orthogonal matrix
, which are contained in the orthogonal matrix ![]() . Thus, the geometry of the ellipsoid can be read from the SED of the PD matrix
. Thus, the geometry of the ellipsoid can be read from the SED of the PD matrix ![]() : the eigenvectors give the principal directions, and the semi-axis lengths are the square root of the eigenvalues.
: the eigenvectors give the principal directions, and the semi-axis lengths are the square root of the eigenvalues.
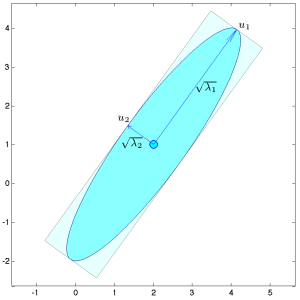 |
The graph on the left shows the ellipsoid |
|
|
|
| The matrix |
|
|
|
|
| with | |
|
|
|
| We check that the columns of |
The above shows in particular that an equivalent representation of an ellipsoid is
![]()
where ![]() is PD.
is PD.
It is possible to define degenerate ellipsoids, which correspond to cases when the matrix ![]() in the above, or its inverse
in the above, or its inverse ![]() , is degenerate. For example, cylinders or slabs (intersection of two parallel half-spaces) are degenerate ellipsoids.
, is degenerate. For example, cylinders or slabs (intersection of two parallel half-spaces) are degenerate ellipsoids.

