Sample variance and standard deviation
The sample variance of given numbers ![]() , is defined as
, is defined as
![]()
where ![]() is the sample average of
is the sample average of ![]() . The sample variance is a measure of the deviations of the numbers
. The sample variance is a measure of the deviations of the numbers ![]() with respect to the average value
with respect to the average value ![]() .
.
The sample standard deviation is the square root of the sample variance, ![]() . It can be expressed in terms of the Euclidean norm of the vector
. It can be expressed in terms of the Euclidean norm of the vector ![]() , as
, as
![]()
where ![]() denotes the Euclidean norm.
denotes the Euclidean norm.
More generally, for any vector ![]() , with
, with ![]() for every
for every ![]() , and
, and ![]() , we can define the corresponding weighted variance as
, we can define the corresponding weighted variance as
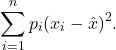
The interpretation of ![]() is in terms of a discrete probability distribution of a random variable
is in terms of a discrete probability distribution of a random variable ![]() , which takes the value
, which takes the value ![]() with probability
with probability ![]() ,
, ![]() . The weighted variance is then simply the expected value of the squared deviation of
. The weighted variance is then simply the expected value of the squared deviation of ![]() from its mean
from its mean ![]() , under the probability distribution
, under the probability distribution ![]() .
.
See also: Sample and weighted average.
