21 APPLICATIONS
21.1. Trilateration by distance measurements
 |
|
|
In many applications such as GPS it is of interest to infer the location of an emitter (for example, a cell phone) from the measurement of distances to known points. These distances are obtained by estimating the differences in time of arrival of a wave front originating from the emitter. In trilateration, only three points are used. We then have to find the intersection of three spheres. The problem can then be reduced to solving a linear equation followed by a quadratic equation in one variable. The multilateration problem, which allows for more than three points, provides more accurate measurements. (Source.) |
|
Denote by ![]() ,
, ![]() the three known points and by
the three known points and by ![]() the measured distances to the emitter. Mathematically the problem is to solve, for a point
the measured distances to the emitter. Mathematically the problem is to solve, for a point ![]() in
in ![]() , the equations
, the equations
![]()
We write them out:
![]()
Let ![]() . The equations above imply that
. The equations above imply that
![]()
Using matrix notation, with ![]() the matrix of points, and
the matrix of points, and ![]() the vector of ones:
the vector of ones:
![]()
Let us assume that the square matrix ![]() is full-rank, that is, invertible. The equation above implies that
is full-rank, that is, invertible. The equation above implies that
![]()
In words: the point lies in a line passing through ![]() and with direction
and with direction ![]() .
.
We can then solve the equation in
![]()
This equation is quadratic in ![]() :
:
![]()
and can be solved in closed-form. The spheres intersect if and only if there is a real, non-negative solution ![]() . Generically, if the spheres have a non-empty intersection, there are two positive solutions, hence two points in the intersection. This is understandable geometrically: the intersection of two spheres is a circle, and intersecting a circle with a third sphere produces two points. The line joining the two points is the line
. Generically, if the spheres have a non-empty intersection, there are two positive solutions, hence two points in the intersection. This is understandable geometrically: the intersection of two spheres is a circle, and intersecting a circle with a third sphere produces two points. The line joining the two points is the line ![]() , as identified above.
, as identified above.
21.2. Estimation of traffic flow
|
The basic traffic flow estimation problem involves inferring the number of cars going through links based on information on the number of cars passing through neighboring links. |
|
For the simple problem above, we simply use the fact that at each intersection, the incoming traffic has to match the outgoing traffic. This leads to the linear equations:

We can write this in matrix format: ![]() with
with
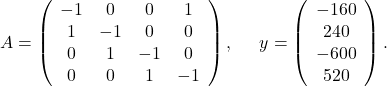
The matrix ![]() is nothing else than the incidence matrix associated with the graph that has the intersections as nodes and links as edges.
is nothing else than the incidence matrix associated with the graph that has the intersections as nodes and links as edges.
