"

A squared linear function

A squared linear function is a quadratic function q: \mathbb{R}^n \rightarrow \mathbb{R} of the form

    \begin{align*} q(x) &= (v^Tx)^2, \end{align*}

for some vector v \in \mathbb{R}^n.

The function vanishes on the space orthogonal to v, which is the hyperplane defined by the single linear equation v^Tx = 0. Thus, in effect this function is really one-dimensional: it varies only along the direction v.

 

 

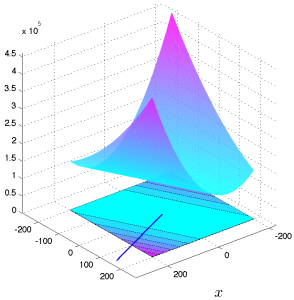Level sets and graph of a dyadic quadratic function, corresponding to the vector v= (2,1). The function is constant along hyperplanes orthogonal to v.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Linear Algebra and Applications Copyright © 2023 by VinUiversity is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book