A theorem on positive semidefinite forms and eigenvalues
Theorem: (Link with SED)
|
A quadratic form |
Proof: Let ![]() be the SED of
be the SED of ![]() .
.
If ![]() , then
, then ![]() gor every
gor every ![]() . Thus, for every
. Thus, for every ![]() :
:
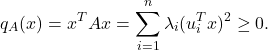
Conversely, if there exist ![]() for which
for which ![]() , then choosing
, then choosing ![]() will result in
will result in ![]() for every
for every ![]() , then the condition
, then the condition
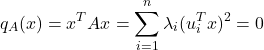
trivially implies ![]() for every
for every ![]() , which can be written as
, which can be written as ![]() .
.
Since ![]() is orthogonal, it is invertible, and we conclude that
is orthogonal, it is invertible, and we conclude that ![]() . Conversely, if
. Conversely, if ![]() for some
for some ![]() , we can achieve
, we can achieve ![]() for some non-zero
for some non-zero ![]() .
.
