APPLICATIONS

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

16 APPLICATIONS

State-space models of linear dynamical systems.

16.1 State-space models of linear dynamical systems.

Definition

Many discrete-time dynamical systems can be modeled via linear state-space equations, of the form

$x(t+1)=Ax(t)+Bu(t), \quad y(t)=Cx(t)+Du(t), \quad t=0,1,2,\dots$

where $x(t) \in \mathbb{R}^{n}$ is the state, which encapsulates the state of the system at time $t, u(t) \in \mathbb{R}^{p}$ contains control variables, $y(t) \in \mathbb{R}^{k}$ contains specific outputs of interest. The matrices

$A \in \mathbb{R}^{n \times n}, \quad B \in \mathbb{R}^{n \times p}, \quad C \in \mathbb{R}^{k \times n}, \quad D \in \mathbb{R}^{k \times p}$

are of appropriate dimensions to ensure compatibility of matrix multiplications.

In effect, a linear dynamical model postulates that the state at the next instant is a linear function of the state at past instants, and possibly other ‘‘exogenous’’ inputs; and that the output is a linear function of the state and input vectors.

A continuous-time model would take the form of a differential equation

$\dfrac{d}{dt}x(t)=Ax(t)+Bu(t), \quad y(t)=Cx(t)+Du(t), \quad t \ge 0.$

Finally, the so-called time-varying models involve time-varying matrices $A, B, C, D$ (see an example below).

Motivation

The main motivation for state-space models is to be able to model high-order derivatives in dynamical equations, using only first-order derivatives, but involving vectors instead of scalar quantities.

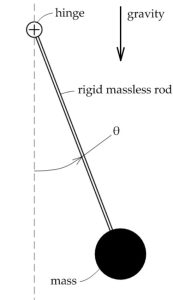
	Consider, for instance, the second-order differential equation:
	$m\ddot{y}(t) + c\dot{y}(t) + ky(t) = u(t)$
	which captures the dynamics of a damped mass-spring system. In this equation:
	$m$ : the mass of the object attached to the spring.
	$c$ : the damping coefficient.
	$k$ : the spring constant
	$u(t)$ : any external force applied to the mass
	$y(t)$ : the vertical displacement of the mass from its equilibrium position.

The above involves second-order derivatives of a scalar function $y(\cdot)$ . We can express it in an equivalent form involving only first-order derivatives, by defining the state vector to be

$x(t) := \begin{pmatrix} y(t) \\ \dot{y}(t) \end{pmatrix}.$

The price we pay is that now we deal with a vector equation instead of a scalar equation:

$\dot{x}(t) = \begin{pmatrix} \dot{y}(t) \\ \ddot{y}(t) \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -\dfrac{k}{m} & -\dfrac{c}{m} \end{pmatrix}x(t) + \begin{pmatrix} 0 \\[0.5ex] \dfrac{1}{m} \end{pmatrix}u(t).$

The position $y(t)$ is a linear function of the state by the relation $y(t) = Cx(t)$ where

$C = (1, 0).$

A nonlinear system

In the case of non-linear systems, we can also use state-space representations. In the case of autonomous systems (no external input) for example, these come in the form

$\dot{x}(t) = f(x(t))$

where $f: \mathbb{R}^{n+p} \rightarrow \mathbb{R}^{n}$ is now a non-linear map. Now assume we want to model the behavior of the system near an equilibrium point $x_{0}$ (such that $f(x_{0}) = 0$ ). Let us assume for simplicity that $x_{0}=0$ .

Using the first-order approximation of the map $f$ , we can write a linear approximation to the above model:

$\dfrac{d}{dt}x(t)=Ax(t), \quad t \ge 0.$

where

$A = \dfrac{\partial f}{\partial x} (0).$

	The pendulum’s motion is governed by the nonlinear equation $\ddot{\theta} = - \sin(\theta)$ , where $\theta$ is the angular displacement from the vertical position and the dot denotes time differentiation.
	To understand the dynamics near $\theta = 0$ and $\theta = \pi$ , we linearize this equation using the first-order Taylor series expansion around a point $a$ :
	$f(x) \approx f(a) + f'(a)(x-a).$
	For $\theta = 0$ , setting $f(x) = \sin(x)$ and $a = 0$ , we find $f'(x) = \cos(x)$ and $f'(0) = 1$ . This gives the approximation $\sin(\theta) \approx \theta$ , resulting in the simplified equation
	$\ddot{\theta} = -\theta.$
	Similarly, for $\theta = \pi$ , setting $a = \pi$ gives $f'(\pi) = -1$ . The linear approximation here is $\sin(\theta) \approx -(\theta - \pi)$ , leading to
	$\ddot{\theta} = \theta - \pi.$
	This linearization elucidates the pendulum’s unstable dynamics at $\theta = \pi$ , assisting in predicting substantial reactions to minor disturbances.