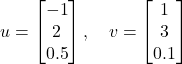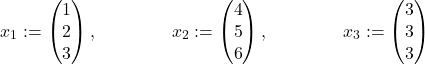1 BASICS
1.1. Definitions
Vectors
Assume we are given a collection of ![]() real numbers,
real numbers, ![]() . We can represent them as
. We can represent them as ![]() locations on a line. Alternatively, we can represent the collection as a single point in a
locations on a line. Alternatively, we can represent the collection as a single point in a ![]() -dimensional space. This is the vector representation of the collection of numbers; each number
-dimensional space. This is the vector representation of the collection of numbers; each number ![]() is called a component or element of the vector.
is called a component or element of the vector.
Vectors can be arranged in a column or a row; we usually write vectors in column format:

We denote by ![]() denotes the set of real vectors with
denotes the set of real vectors with ![]() components. If
components. If ![]() denotes a vector, we use subscripts to denote components, so that
denotes a vector, we use subscripts to denote components, so that ![]() is the
is the ![]() -th component of
-th component of ![]() . Sometimes the notation
. Sometimes the notation ![]() is used to denote the
is used to denote the ![]() -th component.
-th component.
| A vector can also represent a point in a multi-dimensional space |
|
| Example 1: The vector |
|
See also:
Transpose
If ![]() is a column vector,
is a column vector, ![]() denotes the corresponding row vector, and vice-versa. Hence, if
denotes the corresponding row vector, and vice-versa. Hence, if ![]() is the column vector above:
is the column vector above:
![]()
Sometimes we use the looser, in-line notation ![]() , to denote a row or column vector, the orientation being understood from context.
, to denote a row or column vector, the orientation being understood from context.
1.2. Independence
A set of vectors ![]() in
in ![]() is said to be linearly independent if and only if the following condition on a vector
is said to be linearly independent if and only if the following condition on a vector ![]() :
:
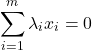
implies ![]() for
for ![]() . This means that no vector in the set can be expressed as a linear combination of the others.
. This means that no vector in the set can be expressed as a linear combination of the others.
| Example 2: the vectors |
1.3. Subspace, span, affine sets
A subspace of ![]() is a subset that is closed under addition and scalar multiplication. Geometrically, subspaces are ‘‘flat’’ (like a line or plane in 3D) and pass through the origin.
is a subset that is closed under addition and scalar multiplication. Geometrically, subspaces are ‘‘flat’’ (like a line or plane in 3D) and pass through the origin.
An important result of linear algebra, which we will prove later, says that a subspace ![]() can always be represented as the span of a set of vectors
can always be represented as the span of a set of vectors ![]() ,
, ![]() , that is, as a set of the form
, that is, as a set of the form
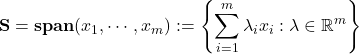
An affine set is a translation of a subspace — it is ‘‘flat’’ but does not necessarily pass through ![]() , as a subspace would. (Think for example of a line, or a plane, that does not go through the origin.) So an affine set
, as a subspace would. (Think for example of a line, or a plane, that does not go through the origin.) So an affine set ![]() can always be represented as the translation of the subspace spanned by some vectors:
can always be represented as the translation of the subspace spanned by some vectors:
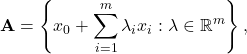
for some vectors ![]() where
where ![]() . In shorthand notation, we write
. In shorthand notation, we write ![]()
| Example 3: In |
|
|
|
|
| is the plane passing through the origin pictured in blue. | |
When ![]() is the span of a single non-zero vector, the set
is the span of a single non-zero vector, the set ![]() is called a line passing through the point
is called a line passing through the point ![]() . Thus, lines have the form
. Thus, lines have the form
![]()
where ![]() determines the direction of the line, and
determines the direction of the line, and ![]() is a point through which it passes.
is a point through which it passes.
| Example 4: A line in |
1.4. Basis, dimension
Basis
A basis of ![]() is a set of
is a set of ![]() independent vectors. If the vectors
independent vectors. If the vectors ![]() form a basis, we can express any vector as a linear combination of the
form a basis, we can express any vector as a linear combination of the ![]() ‘s:
‘s:
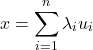
The standard basis (alternatively, natural basis) in ![]() consists of the vectors
consists of the vectors ![]() , where
, where ![]() ‘s components are all zero, except the
‘s components are all zero, except the ![]() -th, which is equal to 1. In
-th, which is equal to 1. In ![]() , we have
, we have
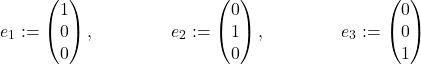
| Example 5: The set of three vectors in |
|
|
| is not independent, since |
Basis of a subspace
The basis of a given subspace ![]() is any independent set of vectors whose span is
is any independent set of vectors whose span is ![]() . If the vectors
. If the vectors ![]() form a basis of
form a basis of ![]() , we can express any vector as a linear combination of the
, we can express any vector as a linear combination of the ![]() ‘s:
‘s:
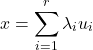
The number of vectors in the basis is actually independent of the choice of the basis (for example, in ![]() you need two independent vectors to describe a plane containing the origin). This number is called the dimension of
you need two independent vectors to describe a plane containing the origin). This number is called the dimension of ![]() . We can accordingly define the dimension of an affine subspace, as that of the linear subspace of which it is a translation.
. We can accordingly define the dimension of an affine subspace, as that of the linear subspace of which it is a translation.
Examples:
- The dimension of a line is 1 since a line is of the form
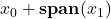 for some non-zero vector
for some non-zero vector 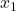 .
. - Dimension of an affine subspace.