Edge weight matrix of a graph
A symmetric matrix is a way to describe a weighted, undirected graph: each edge in the graph is assigned a weight ![]() . Since the graph is undirected, the edge weight is independent of the direction (from
. Since the graph is undirected, the edge weight is independent of the direction (from ![]() to
to ![]() or vice-versa). Hence,
or vice-versa). Hence, ![]() is symmetric.
is symmetric.
See also: Arc-node incidence matrix of a graph.
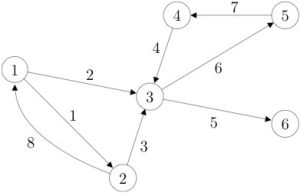
![Rendered by QuickLaTeX.com W=\left[\begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \end{array}\right]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5055c982a9287c9cdc6c7469495006dd_l3.png)
