Dimension of an affine subspace
The set ![]() in
in ![]() defined by the linear equations
defined by the linear equations
![]()
is an affine subspace of dimension ![]() . The corresponding linear subspace is defined by the linear equations obtained from the above by setting the constant terms to zero:
. The corresponding linear subspace is defined by the linear equations obtained from the above by setting the constant terms to zero:
![]()
We can solve for ![]() and get
and get ![]() . We obtain a representation of the linear subspace as the set of vectors
. We obtain a representation of the linear subspace as the set of vectors ![]() that have the form
that have the form
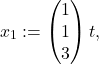
for some scalar ![]() . Hence the linear subspace is the span of the vector
. Hence the linear subspace is the span of the vector ![]() , and is of dimension
, and is of dimension ![]() .
.
We obtain a representation of the original affine set by finding a particular solution ![]() , by setting say
, by setting say ![]() and solving for
and solving for ![]() . We obtain
. We obtain
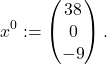
The affine subspace ![]() is thus the line
is thus the line ![]() , where
, where ![]() are defined above.
are defined above.
