8 EXERCISES
- Subspaces
- Projections, scalar products, angles
- Orthogonalization
- Generalized Cauchy-Schwarz inequalities
- Linear functions
8.1. Subspaces
1. Consider the set ![]() of points such that
of points such that
![]()
Show that ![]() is a subspace. Determine its dimension, and find a basis for it.
is a subspace. Determine its dimension, and find a basis for it.![]()
2. Consider the set in ![]() , defined by the equation
, defined by the equation
![]()
a. Show that the set ![]() is an affine subspace of dimension
is an affine subspace of dimension ![]() . To this end, express it as
. To this end, express it as
![]()
where ![]() , and
, and ![]() are independent vectors.
are independent vectors.
b. Find the minimum Euclidean distance from ![]() to the set
to the set ![]() . Find a point that achieves the minimum distance. (Hint: using the Cauchy-Schwarz inequality, prove that the minimum-distance point is proportional to
. Find a point that achieves the minimum distance. (Hint: using the Cauchy-Schwarz inequality, prove that the minimum-distance point is proportional to ![]() .)
.)
8.2. Projections, scalar product, angles
1. Find the projection ![]() of the vector
of the vector ![]() on the line that passes through
on the line that passes through ![]() with direction given by the vector
with direction given by the vector ![]()
2. Find the Euclidean projection of a point ![]() on a hyperplane
on a hyperplane
![]()
where ![]() and
and ![]() are given.
are given.![]()
3. Determine the angle between the following two vectors:
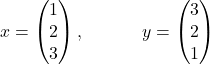
Are these vectors linearly independent?
8.3. Orthogonalization
Let ![]() be two unit-norm vectors, that is, such that
be two unit-norm vectors, that is, such that ![]() . Show that the vectors
. Show that the vectors ![]() and
and ![]() are orthogonal. Use this to find an orthogonal basis for the subspace spanned by
are orthogonal. Use this to find an orthogonal basis for the subspace spanned by ![]() and
and ![]() .
.
8.4. Generalized Cauchy-Schwarz inequalities
1. Show that the following inequalities hold for any vector ![]() :
:
![]()
2. Show that following inequalities hold for any vector:
![]()
Hint: use the Cauchy-Schwarz inequality for the second inequality.
3. In a generalized version of the above inequalities, show that for any non-zero vector ![]() ,
,
![]()
where ![]() is the cardinality of the vector
is the cardinality of the vector ![]() , defined as the number of non-zero elements in
, defined as the number of non-zero elements in ![]() For which vectors
For which vectors ![]() is the upper bound attained?
is the upper bound attained?
8.5. Linear functions
1. For a ![]() -vector
-vector ![]() , with
, with ![]() odd, we define the median of
odd, we define the median of ![]() as
as ![]() . Now consider the function
. Now consider the function ![]() , with values
, with values
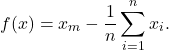
Express ![]() as a scalar product, that is, find
as a scalar product, that is, find ![]() such that
such that ![]() for every
for every ![]() . Find a basis for the set of points
. Find a basis for the set of points ![]() such that
such that ![]() .
.![]()
2. For ![]() , we consider the ‘‘power-law’’ function
, we consider the ‘‘power-law’’ function ![]() , with values
, with values
![]()
Justify the statement: ‘‘the coefficients ![]() provide the ratio between the relative error in
provide the ratio between the relative error in ![]() to a relative error in
to a relative error in ![]() ’’.
’’.![]()
3. Find the gradient of the function ![]() that gives the distance from a given point
that gives the distance from a given point ![]() to a point
to a point ![]() .
.
