EXERCISES

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

40 EXERCISES

40.1. SVD of simple matrices

1. Consider the matrix

$\begin{align*} A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} \end{align*}$

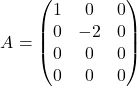
a. Find the range, nullspace, and rank of $A$ .

b. Find an SVD of $A$ .

c. Determine the set of solutions to the linear equation $Ax=y$ , with

$\begin{center} \[ y=\left(\begin{array}{l} 2 \\ 3 \\ 0 \\ 0 \end{array}\right), \quad y=\left(\begin{array}{l} 2 \\ 0 \\ 0 \\ 3 \end{array}\right). \] \end{center}$

2. Consider the $2 \times 2$ matrix

$\begin{center} \[ A=\frac{1}{\sqrt{10}}\left(\begin{array}{l} 2 \\ 1 \end{array}\right)\left(\begin{array}{ll} 1 & -1 \end{array}\right)+\frac{2}{\sqrt{10}}\left(\begin{array}{c} -1 \\ 2 \end{array}\right)\left(\begin{array}{ll} 1 & 1 \end{array}\right). \] \end{center}$

a. What is an SVD of $A$ ? Express it as $A = USV^T$ , with $S$ the diagonal matrix of singular values ordered in decreasing fashion. Make sure to check all the properties required for $U,S,V$ .

b. Find the semi-axis lengths and principal axes (minimum and maximum distance and associated directions from $\mathcal{E}$ to the center) of the ellipsoid

$\begin{center} \[ \mathcal{E}(A) = \{Ax: x \in \mathbb{R}^2, ||x||_2 \leq 1\}. \] \end{center}$

Hint: Use the SVD of $A$ to show that every element of $\mathcal{E}(A)$ is of the form $y = U \overline{y}$ for some element $\overline{y}$ in $\mathcal{E}(S)$ . That is, $\mathcal{E}(A) = \{U\overline{y}: \overline{y} \in \mathcal{E}(S)\}$ . (In other words, the matrix $U$ maps $\mathcal{E}(S)$ into the set $\mathcal{E}(A)$ .) Then analyze the geometry of the simpler set $\mathcal{E}(S)$ .

c. What is the set $\mathcal{E}(A)$ when we append a zero vector after the last column of $A$ , that is $A$ is replaced with $\tilde{A} = (A, 0) \in \mathbb{R}^{2 \times 3}$ ?

d. The same question when we append a row after the last row of $A$ , that is, $A$ is replaced with $\tilde{A} = [A^T, 0]^T \in \mathbb{R}^{3 \times 2}$ . Interpret geometrically your result.

40.2. Rank and SVD

The image on the left shows a $256 \times 256$ matrix $A$ of pixel values. The lines indicate $+1$ values; at each intersection of lines, the corresponding matrix element is $+2$ . All the other elements are zero.

1. Show that for some permutation matrices $P, Q$ , the permuted matrix $B: = PAQ$ has the symmetric form $B = pq^T + qp^T$ , for two vectors $p, q$ . Determine $P, Q, B$ and $p, q$ .

2. What is the rank of $A$ ? Hint: find the nullspace of $B$ .

3. Find an SVD of $A$ . Hint: Find an eigenvalue decomposition of $S$ , using the results of an exercise on eigenvalue here.

40.3. Procrustes problem

The Orthogonal Procrustes problem is a problem of the form

$\begin{align*} \min\limits_{X} ||AX-B||_F: X^TX = I_p, \end{align*}$

where $||\cdot||_F$ denotes the Frobenius norm, and the matrices $A \in \mathbb{R}^{m \times n}$ , $B \in \mathbb{R}^{m \times p}$ are given. Here, the matrix variable $X \in \mathbb{R}^{n \times p}$ is constrained to have orthonormal columns. When $n=m=p$ , the problem can be interpreted geometrically as seeking a transformation of points (contained in $A$ ) to other points (contained in $B$ ) that involves only rotation.

1. Show that the solution to the Procrustes problem above can be found via the SVD of the matrix $A^TB$ .

2. Derive a formula for the answer to the constrained least-squares problem

$\begin{align*} \min\limits_{x} ||Ax-b||_2: ||x||_2=1, \end{align*}$

with $A \in \mathbb{R}^{m \times n}$ , $b \in \mathbb{R}^m$ given.

40.4. SVD and projections

1. We consider a set of $m$ data points $x_i \in \mathbb{R}^n$ , $i = 1, \cdots, m$ . We seek to find a line in $\mathbb{R}^n$ such that the sum of the squares of the distances from the points to the line is minimized. To simplify, we assume that the line goes through the origin.

a. Consider a line that goes through the origin $\mathcal{L} = \{tu: t\in\mathbb{R}\}$ , where $u \in \mathbb{R}^n$ is given. (You can assume without loss of generality that $||u||_2=1$ .) Find an expression for the projection of a given point $x$ on $\mathcal{L}$ .

b. Now consider the $m$ points and find an expression for the sum of the squares of the distances from the points to the line $\mathcal{L}$ .

c. Explain how you would find the line via the SVD of the $n\times m$ matrix $X = [x_1, \cdots, x_m]$ .

d. How would you address the problem without the restriction that the line has to pass through the origin?

2. Solve the same problems as previously by replacing the line with a hyperplane.

40.5. SVD and least-squares

1. Consider the matrix $A$ formed as $A = (c_1, c_2, c_3)$ , with

$\begin{align*} c_1 &= (1, 2, 8), \quad c_2 = (3, 6, 9), \quad c_3 = c_1 - 4c_2 + \epsilon_1 v, \quad \epsilon_1 = .0000001, \end{align*}$

with $v$ is a vector chosen randomly in $[-0.5, 0.5]^3$ (this represents a 3-dimensional cube with each dimension ranging from $-0.5$ to $0.5$ ). In addition, we define

$\begin{align*} y = 2c_1 - 7c_2 + \epsilon_2 w, \quad \epsilon_2 = .0001, \end{align*}$

with again $w$ chosen randomly in $[-0.5, 0.5]^3$ . We consider the associated least-squares problem

$\begin{align*} \min\limits_x ||Ax-y||_2. \end{align*}$

a. What is the rank of $A$ ?

b. Apply the least-squares formula $x^* = (A^TA)^{-1}A^Ty$ . What is the norm of the residual vector, $r = Ax-y$ ?

c. Express the least-squares solution in terms of the SVD of $A$ . That is, form the pseudo-inverse of $A$ and apply the formula $x^* = A^{\dagger} y$ . What is now the norm of the residual?

d. Interpret your results.

2. Consider a least-squares problem

$\begin{align*} \min\limits_x ||Ax-y||_2 \end{align*}$

where the data matrix $A \in \mathbb{R}^{m \times n}$ has rank one.

a. Is the solution unique?

b. Show how to reduce the problem to one involving one scalar variable.

c. Express the set of solutions in closed form.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License