EXISTENCE AND UNICITY OF SOLUTIONS

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

19 EXISTENCE AND UNICITY OF SOLUTIONS

19.1. Set of solutions

Consider the linear equation in $x \in \mathbb{R}^n$ :

$\begin{align*}Ax = y,\end{align*}$

where $A \in \mathbb{R}^{m \times n}$ and $y \in \mathbb{R}^m$ are given, and $x \in \mathbb{R}^n$ is the variable.

The set of solutions to the above equation, if it is not empty, is an affine subspace. That is, it is of the form $x_0 + L$ where $L$ is a subspace.

We’d like to be able to

determine if a solution exists;
if so, determine if it is unique;
compute a solution 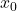$x_0$ if one exists;
find an orthonormal basis of the subspace $L$ .

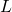19.2. Existence: range and rank of a matrix

Range

The range (or, image) of a $m \times n$ matrix $A$ is defined as the following subset of $\mathbb{R}^m$ :

$\begin{align*} \mathbf{R}(A) := \{Ax : x \in \mathbb{R}^n\}. \end{align*}$

The range describes the vectors $y = Ax$ that can be attained in the output space by an arbitrary choice of a vector $x$ , in the input space. The range is simply the span of the columns of $A$ .

If $y \not \in \mathbf{R}(A)$ , we say that the linear equation $Ax = y$ is infeasible. The set of solutions to the linear equation is empty.

From a matrix $A$ it is possible to find a matrix, the columns of which span the range of the matrix $A$ , and are mutually orthogonal. Hence, $U^TU = I_r$ , where $r$ is the dimension of the range. One algorithm to obtain the matrix $U$ is the Gram-Schmidt procedure.

Example: An infeasible linear system.

Rank

The dimension of the range is called the rank of the matrix. As we will see later, the rank cannot exceed any one of the dimensions of the matrix $A: r \leq \mathrm{min}(m, n)$ . A matrix is said to be full rank if $r = \mathrm{min}(m, n)$ .

Note that the rank is a very ‘‘brittle’’ notion, in that small changes in the entries of the matrix can dramatically change its rank. Random matrices are full rank. We will develop here a better, more numerically reliable notion.

Example 1: Range and rank of a simple matrix.

Let’s consider the matrix

$A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}.$

Range: The columns of $A$ are

$c_1 = \begin{pmatrix} 1 \\ 3 \end{pmatrix}, \quad c_2 = \begin{pmatrix} 2 \\ 4 \end{pmatrix}.$

Any linear combination of these vectors can be represented as $Ax$ , where $x \in \mathbb{R}^2$ . For our matrix $A$ , the range can be visually represented as the plane spanned by $c_1$ and $c_2$ .

Rank: The rank of a matrix is the dimension of its range. For our matrix $A$ , since both column vectors are linearly independent, the rank is:

$\text{rank}(A) = 2.$

Thus, the matrix $A$ is of full rank.

See also:

Full row rank matrices

The matrix $A$ is said to be full row rank (or, onto) if the range is the whole output space, $\mathbb{R}^m$ . The name ‘‘full row rank’’ comes from the fact that the rank equals the row dimension of $A$ . Since the rank is always less than the smallest of the number of columns and rows, a $m \times n$ matrix of full row rank has necessarily less rows than columns (that is, $m \leq n$ ).

An equivalent condition for $A$ to be full row rank is that the square, $m \times m$ matrix $AA^T$ is invertible, meaning that it has full rank, $m$ .

Proof.

19.3. Unicity: nullspace of a matrix

Nullspace

The nullspace (or, kernel) of a $m \times n$ matrix $A$ is the following subspace of $\mathbb{R}^n$ :

$\begin{align*} \mathbf{N}(A) := \{ x \in \mathbb{R}^n : Ax = 0 \}. \end{align*}$

The nullspace describes the ambiguity in $x$ given $y = Ax$ : any $z \in \mathbf{N}(A)$ will be such that $A(x+z) = y$ , so $x$ cannot be determined by the sole knowledge of $y$ if the nullspace is not reduced to the singleton $\{0\}$ .

From a matrix $A$ we can obtain a matrix, the columns of which span the nullspace of the matrix $A$ , and are mutually orthogonal. Hence, $U^TU = I_p$ , where $p$ is the dimension of the nullspace.

Example 2: Nullspace of a simple matrix.

Consider the matrix

$A = \begin{pmatrix} 1 & 2 & 1\\ 2 & 4 & 2 \end{pmatrix}.$

The nullspace, $\mathbf{N}(A)$ , is defined as

$\mathbf{N}(A) = \{ x \in \mathbb{R}^3 : Ax = 0 \}.$

Given the matrix structure, for any vector $x$ such that the first component is $-2$ times the second component and the third component can be arbitrary, $Ax = 0$ .

For example, the vector

$x = \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix},$

satisfies $Ax = 0$ and is thus in the nullspace of $A$ . The dimension of this nullspace, $p$ , is 2 (since we have two free variables).

Nullity

The nullity of a matrix is the dimension of the nullspace. The rank-nullity theorem states that the nullity of a $m \times n$ matrix $A$ is $n - r$ , where $r$ is the rank of $A$ .

Full column rank matrices

The matrix $A$ is said to be full column rank (or, one-to-one) if its nullspace is the singleton $\{0\}$ . In this case, if we denote by $a_i$ the $n$ columns of $A$ , the equation

$\begin{align*} (Ax =) \sum_{i=1}^n a_ix_i = 0 \end{align*}$

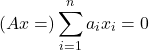
has $x = 0$ as the unique solution. Hence, $A$ is one-to-one if and only if its columns are independent. Since the rank is always less than the smallest of the number of columns and rows, a $m \times n$ matrix of full column rank has necessarily less columns than rows (that is, $m \geq n$ ).

The term ‘‘one-to-one’’ comes from the fact that for such matrices, the condition $y = Ax$ uniquely determines $x$ , since $Ax_1 = y$ and $Ax_2 = y$ implies $A(x_1 - x_2) = 0$ , so that the solution is unique: $x_1 = x_2$ . The name ‘‘full column rank’’ comes from the fact that the rank equals the column dimension of $A$ .

An equivalent condition for $A$ to be full column rank is that the square, $n \times n$ matrix $A^TA$ is invertible, meaning that it has full rank, $n$ .

Proof

Example: Nullspace of a transpose incidence matrix.

19.4. Fundamental facts

Two important results about the nullspace and range of a matrix.

Rank-nullity theorem

The nullity (dimension of the nullspace) and the rank (dimension of the range) of a $m \times n$ matrix $A$ add up to the column dimension of $A, n$ .

Proof.

Another important result is involves the definition of the orthogonal complement of a subspace.

Fundamental theorem of linear algebra

The range of a matrix is the orthogonal complement of the nullspace of its transpose. That is, for a $m \times n$ matrix $A$ :

$\begin{align*} \mathbf{R}(A)^{\perp} = \mathbf{N}(A^T) \end{align*}$

Proof.


	The figure provides a sketch of the proof: consider a $3 \times 2$ matrix, and denote by $a_i \in \mathbb{R}^3 (i = 1, 2)$ its rows, so that
	$\begin{align} \begin{pmatrix} a_1 & a_2 \end{pmatrix}, \quad A^T = \begin{pmatrix} a_1^T \\[1ex] a_2^T \end{pmatrix}. \end{align}$
	Then $A^Tx = 0$ if and only if $a_i^Tx = 0, i = 1, 2$ . In words: $x$ is in the nullspace of $A^T$ if and only if it is orthogonal to the vectors $a_i \, (i = 1, 2)$ . But those two vectors span the range of $A$ , hence $x$ is orthogonal to any element in the range.