Gradient of a function
The gradient of a differentiable function ![]() contains the first derivatives of the function with respect to each variable. The gradient is useful to find the linear approximation of the function near a point.
contains the first derivatives of the function with respect to each variable. The gradient is useful to find the linear approximation of the function near a point.
Definition
The gradient of ![]() at
at ![]() , denoted
, denoted ![]() , is the vector in
, is the vector in ![]() given by
given by
![Rendered by QuickLaTeX.com \[ \nabla f\left(x_0\right) = \left(\begin{array}{c} \dfrac{\partial f}{\partial x_1}(x) \\[0.5em] \vdots \\[0.5em] \dfrac{\partial f}{\partial x_n}(x) \end{array}\right). \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7707a895c6fb3bab740e3f419125f724_l3.png)
Examples:
- Distance function: The distance function from a point
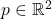 to another point
to another point 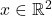 is defined as
is defined as
![]()
The function is differentiable, provided ![]() , which we assume. Then
, which we assume. Then
![Rendered by QuickLaTeX.com \[\nabla \rho(x)=\frac{1}{\sqrt{\left(x_1-p_1\right)^2+\left(x_2-p_2\right)^2}}\left(\begin{array}{l} x_1-p_1 \\ x_2-p_2 \end{array}\right) .\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bf9581eb729dc1f9f229f2b4bffd2952_l3.png)
- Log-sum-exp function: Consider the ‘‘log-sum-exp’’ function
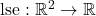 , with values
, with values
![]()
The gradient of ![]() at
at ![]() is
is
![]()
where ![]() . More generally, the gradient of the function
. More generally, the gradient of the function ![]() with values
with values
![Rendered by QuickLaTeX.com \[\operatorname{lse}(x)=\log \left(\sum_{i=1}^n e^{x_i}\right)\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-828ee245a60f7e0dde16e26d9c2f5ef2_l3.png)
is given by
![Rendered by QuickLaTeX.com \[\nabla f(x)=\frac{1}{\sum_{i=1}^n e^{x_i}}\left(\begin{array}{c} e^{x_1} \\ \ldots \\ e^{x_n} \end{array}\right)=\frac{1}{Z} z,\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-85250c5a70df1b1a516a1c77c27fd154_l3.png)
where 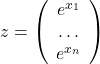 , and
, and ![]() .
.
Composition rule with an affine function
If ![]() is a matrix, and
is a matrix, and ![]() is a vector, the function
is a vector, the function ![]() with values
with values
![]()
is called the composition of the affine map ![]() with
with ![]() with
with ![]() . Its gradient is given by
. Its gradient is given by
![]()
Geometric interpretation
Geometrically, the gradient can be read on the plot of the level set of the function. Specifically, at any point ![]() , the gradient is perpendicular to the level set and points outwards from the sub-level set (that is, it points towards higher values of the function).
, the gradient is perpendicular to the level set and points outwards from the sub-level set (that is, it points towards higher values of the function).

