Hessian of a function
Definition
The Hessian of a twice-differentiable function ![]() at a point
at a point ![]() is the matrix containing the second derivatives of the function at that point. That is, the Hessian is the matrix with elements given by
is the matrix containing the second derivatives of the function at that point. That is, the Hessian is the matrix with elements given by
![]()
The Hessian of ![]() at
at ![]() is often denoted
is often denoted ![]() .
.
The second derivative is independent of the order in which derivatives are taken. Hence, ![]() for every pair
for every pair ![]() . Thus, the Hessian is a symmetric matrix.
. Thus, the Hessian is a symmetric matrix.
Examples
Hessian of a quadratic function
Consider the quadratic function
![]()
The Hessian of ![]() at
at ![]() is given by
is given by
![Rendered by QuickLaTeX.com \begin{align*} \frac{\partial^2 q}{\partial x_i \partial x_j}(x) = \left(\begin{array}{cc} \dfrac{\partial^2 q}{\partial x_1^2}(x) & \dfrac{\partial^2 q}{\partial x_1 \partial x_2}(x) \\[3ex] \dfrac{\partial^2 q}{\partial x_2 \partial x_1}(x) & \dfrac{\partial^2 q}{\partial x_2^2}(x) \end{array}\right) = \left(\begin{array}{ll} 2 & 2 \\ 2 & 6 \end{array}\right) \text{. } \end{align*}](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7da34e3254eaf10d3d614d7b84063455_l3.png)
For quadratic functions, the Hessian is a constant matrix, that is, it does not depend on the point at which it is evaluated.
Hessian of the log-sum-exp function
Consider the ‘‘log-sum-exp’’ function ![]() , with values
, with values
![]()
The gradient of ![]() at
at ![]() is
is
![]()
where ![]() ,
, ![]() . The Hessian is given by
. The Hessian is given by
![]()
More generally, the Hessian of the function ![]() with values
with values
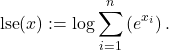
is as follows.
● First the gradient at a point ![]() is (see here):
is (see here):
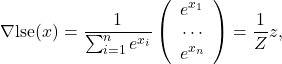
where 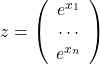 , and
, and ![]() .
.
● Now the Hessian at a point ![]() is obtained by taking derivatives of each component of the gradient. If
is obtained by taking derivatives of each component of the gradient. If ![]() is the
is the ![]() -th component, that is,
-th component, that is,
![]()
then
![]()
and, for ![]() :
:
![]()
More compactly:
![]()
