Incidence matrix of a network
Mathematically speaking, a network is a graph of ![]() nodes connected by
nodes connected by ![]() directed arcs. Here, we assume that arcs are ordered pairs, with at most one arc joining any two nodes; we also assume that there are no self-loops (arcs from a node to itself). We do not assume that the edges of the graph are weighted—they are all similar.
directed arcs. Here, we assume that arcs are ordered pairs, with at most one arc joining any two nodes; we also assume that there are no self-loops (arcs from a node to itself). We do not assume that the edges of the graph are weighted—they are all similar.
We can fully describe the network with the so-called arc-node incidence matrix, which is the ![]() matrix defined as
matrix defined as
![Rendered by QuickLaTeX.com \[ A_{ij} = \left\{ \begin{array}{ll} 1 & \text{if arc } j \text{ starts at node } i \\ -1 & \text{if arc } j \text{ ends at node } i \\ 0 & \text{otherwise.} \end{array} \right. , \quad 1 \le i \le m, \quad 1 \le j \le n. \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-789ad25e589ca5325a972bd07961f645_l3.png)
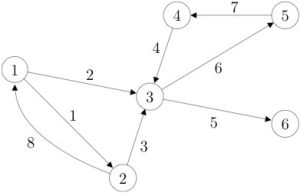 |
The figure shows the graph associated with the arc-node incidence matrix
|
See also: Network flow.
![Rendered by QuickLaTeX.com \[ A = \left[ \begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\ \end{array} \right]. \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ecc6ac49b1215ac8e34b548c9e783d6a_l3.png)
