6 LINEAR FUNCTIONS
6.1. Linear and affine functions
Definition
Linear functions are functions which preserve scaling and addition of the input argument. Affine functions are ‘‘linear plus constant’’ functions.
Formal definition, linear and affine functions. A function ![]() is linear if and only if
is linear if and only if ![]() preserves scaling and addition of its arguments:
preserves scaling and addition of its arguments:
- for every
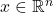 , and
, and 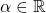 ,
, 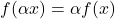 ; and
; and - for every
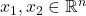 ,
, 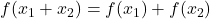 .
.
A function ![]() is affine if and only if the function
is affine if and only if the function ![]() with values
with values ![]() is linear.
is linear.
An alternative characterization of linear functions:
|
A function 1. – For every – For every 2.
3.
|
| Example 1: Consider the functions |
|
|
|
|
|
|
| The function |
Connection with vectors via the scalar product
The following shows the connection between linear functions and scalar products.
Theorem: Representation of affine function via the scalar product
|
A function
for some unique pair |
The theorem shows that a vector can be seen as a (linear) function from the ‘‘input“ space ![]() to the ‘‘output” space
to the ‘‘output” space ![]() . Both points of view (matrices as simple collections of numbers, or as linear functions) are useful.
. Both points of view (matrices as simple collections of numbers, or as linear functions) are useful.
Gradient of an affine function
The gradient of a function ![]() at a point
at a point ![]() , denoted
, denoted ![]() , is the vector of first derivatives with respect to
, is the vector of first derivatives with respect to ![]() (see here for a formal definition and examples). When
(see here for a formal definition and examples). When ![]() (there is only one input variable), the gradient is simply the derivative.
(there is only one input variable), the gradient is simply the derivative.
An affine function ![]() , with values
, with values ![]() has a very simple gradient: the constant vector
has a very simple gradient: the constant vector ![]() . That is, for an affine function
. That is, for an affine function ![]() , we have for every
, we have for every ![]() :
:
![]()
| Example 2: gradient of a linear function: |
| Consider the function |
|
|
| For a given |
|
|
| The level sets are hyperplanes, and are orthogonal to the gradient. |
Interpretations
The interpretation of ![]() are as follows.
are as follows.
- The
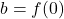 is the constant term. For this reason, it is sometimes referred to as the bias, or intercept (as it is the point where
is the constant term. For this reason, it is sometimes referred to as the bias, or intercept (as it is the point where 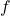 intercepts the vertical axis if we were to plot the graph of the function).
intercepts the vertical axis if we were to plot the graph of the function). - The terms
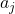 ,
, 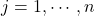 , which correspond to the gradient of
, which correspond to the gradient of 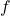 , give the coefficients of influence of
, give the coefficients of influence of 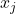 on
on 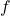 . For example, if
. For example, if 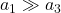 , then the first component of
, then the first component of 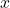 has much greater influence on the value of
has much greater influence on the value of 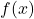 than the third.
than the third.
See also: Beer-Lambert law in absorption spectrometry.
6.2. First-order approximation of non-linear functions
Many functions are non-linear. A common engineering practice is to approximate a given non-linear map with a linear (or affine) one, by taking derivatives. This is the main reason for linearity to be such an ubiquituous tool in Engineering.
One-dimensional case
Consider a function of one variable ![]() , and assume it is differentiable everywhere. Then we can approximate the values function at a point
, and assume it is differentiable everywhere. Then we can approximate the values function at a point ![]() near a point
near a point ![]() as follows:
as follows:
![]()
where ![]() denotes the derivative of
denotes the derivative of ![]() at
at ![]() .
.
Multi-dimensional case
With more than one variable, we have a similar result. Let us approximate a differentiable function ![]() by a linear function
by a linear function ![]() , so that
, so that ![]() and
and ![]() coincide up and including to the first derivatives. The corresponding approximation
coincide up and including to the first derivatives. The corresponding approximation ![]() is called the first-order approximation to
is called the first-order approximation to ![]() at
at ![]() .
.
The approximate function ![]() must be of the form
must be of the form
![]()
where ![]() and
and ![]() . Our condition that
. Our condition that ![]() coincides with
coincides with ![]() up and including to the first derivatives shows that we must have
up and including to the first derivatives shows that we must have
![]()
where ![]() the gradient of
the gradient of ![]() at
at ![]() . Solving for
. Solving for ![]() we obtain the following result:
we obtain the following result:
Theorem: First-order expansion of a function.
|
The first-order approximation of a differentiable function where |
| Example 3: a linear approximation to a non-linear function |
| Consider the log-sum-exp function |
|
|
| admits the gradient at the point |
|
|
| Hence |
|
|
6.3. Other sources of linear models
Linearity can arise from a simple change of variables. This is best illustrated with a specific example.
Example: Power laws.
![Rendered by QuickLaTeX.com \begin{align*} \nabla f = \left(\begin{array}{c} \dfrac{\partial f}{\partial x_1}(x) \\[1em] \dfrac{\partial f}{\partial x_2}(x) \end{array} \right) = \left(\begin{array}{c} 1 \\ 2 \end{array} \right). \end{align*}](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-00791e081d35bf369d9b5a8ad0310183_l3.png)