Linear regression via least squares
Linear regression is based on the idea of fitting a linear function through data points.
In its basic form, the problem is as follows. We are given data ![]() where
where ![]() is the ‘‘input’’ and
is the ‘‘input’’ and ![]() is the ‘‘output’’ for the
is the ‘‘output’’ for the 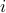 -th measurement. We seek to find a linear function
-th measurement. We seek to find a linear function ![]() such that
such that ![]() are collectively close to the corresponding values
are collectively close to the corresponding values ![]() .
.
In least-squares regression, the way we evaluate how well a candidate function ![]() fits the data is via the (squared) Euclidean norm:
fits the data is via the (squared) Euclidean norm:
![]()
Since a linear function ![]() has the form
has the form ![]() for some
for some ![]() , the problem of minimizing the above criterion takes the form
, the problem of minimizing the above criterion takes the form
![]()
We can formulate this as a least-squares problem:
![]()
where
![Rendered by QuickLaTeX.com \[A=\left(\begin{array}{c} x_1^T \\ \vdots \\ x_m^T \end{array}\right)\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ff92dd4466175e15383e56e7507c6d15_l3.png)
The linear regression approach can be extended to multiple dimensions, that is, to problems where the output in the above problem contains more than one dimension (see here). It can also be extended to the problem of fitting non-linear curves.
See also:

