10 MATRIX-VECTOR AND MATRIX-MATRIX MULTIPLICATION, SCALAR PRODUCT
10.1. Matrix-vector product
Definition
We define the matrix-vector product between a ![]() matrix and a
matrix and a ![]() -vector
-vector ![]() , and denote by
, and denote by ![]() , the
, the ![]() -vector with
-vector with ![]() -th component
-th component
![Rendered by QuickLaTeX.com \[(Ax)_{i}=\sum_{j=1}^{n}A_{ij}x_{j}, i=1,\dots,m.\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-39196c108ce8b8f1d44932dd842c69bf_l3.png)
| The picture on the left shows a symbolic example with |
|
|
|
|
|
|
|
|
|
Interpretation as linear combinations of columns
If the columns of ![]() are given by the vectors
are given by the vectors ![]() so that
so that ![]() , then
, then ![]() can be interpreted as a linear combination of these columns, with weights given by the vector
can be interpreted as a linear combination of these columns, with weights given by the vector ![]() :
:
![]()
| In the above symbolic example, we have |
|
|
|
|
See also:
Interpretation as scalar products with rows
Alternatively, if the rows of ![]() are the row vectors
are the row vectors ![]() :
:
![Rendered by QuickLaTeX.com \[A = \begin{pmatrix} a_{1}^{T} \\ \vdots \\ a_{m}^{T} \end{pmatrix},\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cfbe8fa25c3e32d95b5f44ab358b383f_l3.png)
then ![]() is the vector with elements
is the vector with elements ![]() :
:
![Rendered by QuickLaTeX.com \[Ax = \begin{pmatrix} a_{1}^{T}x \\ \vdots \\ a_{m}^{T}x \end{pmatrix}.\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0d54b8e614e79aebb4a94e32476d318b_l3.png)
| In the above symbolic example, we have |
|
|
|
|
|
|
|
|
|
Left product
If ![]() , then the notation
, then the notation ![]() is the row vector of size
is the row vector of size ![]() equal to the transpose of the column vector
equal to the transpose of the column vector ![]() . That is:
. That is:
![]()
Example: Return to the network example, involving a ![]() incidence matrix. We note that, by construction, the columns of
incidence matrix. We note that, by construction, the columns of ![]() sum to zero, which can be compactly written as
sum to zero, which can be compactly written as ![]() , or
, or ![]() .
.
10.2. Matrix-matrix product
Definition
We can extend the matrix-vector product to the matrix-matrix product, as follows. If ![]() and
and ![]() , the notation
, the notation ![]() denotes the
denotes the ![]() matrix with
matrix with ![]() element given by
element given by
![Rendered by QuickLaTeX.com \[(AB)_{ij} = \sum_{k=1}^{n}A_{ik}B_{kj}.\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5f2c7d1df13e109c04ace92b5a7168f8_l3.png)
Transposing a product changes the order, so that ![]()
Column-wise interpretation
If the columns of ![]() are given by the vectors
are given by the vectors ![]() , with
, with ![]() , so that
, so that ![]() , then
, then ![]() can be written as
can be written as
![]()
In other words, ![]() results from transforming each column
results from transforming each column ![]() of
of ![]() into
into ![]() .
.
Row-wise interpretation
The matrix-matrix product can also be interpreted as an operation on the rows of ![]() . Indeed, if
. Indeed, if ![]() is given by its rows
is given by its rows ![]() then
then ![]() is the matrix obtained by transforming each one of these rows via
is the matrix obtained by transforming each one of these rows via ![]() , into
, into ![]() :
:
![Rendered by QuickLaTeX.com \[AB = \begin{pmatrix}a_{1}^{T} \\ \vdots \\ a_{m}^{T}\end{pmatrix}B= \begin{pmatrix}a_{1}^{T}B \\ \vdots \\ a_{m}^{T}B\end{pmatrix}.\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-78faf8bcf958b1266f77c3985f509d03_l3.png)
(Note that ![]() ‘s are indeed row vectors, according to our matrix-vector rules.)
‘s are indeed row vectors, according to our matrix-vector rules.)
10.3. Block Matrix Products
Matrix algebra generalizes to blocks, provided block sizes are consistent. To illustrate this, consider the matrix-vector product between a ![]() matrix
matrix ![]() and a
and a ![]() -vector
-vector ![]() , where
, where ![]() are partitioned in blocks, as follows:
are partitioned in blocks, as follows:
![]()
where ![]() is
is ![]() Then
Then ![]()
Symbolically, it’s as if we would form the ‘‘scalar’’ product between the ‘‘row vector ![]() and the column vector
and the column vector ![]() !
!
Likewise, if a ![]() matrix
matrix ![]() is partitioned into two blocks
is partitioned into two blocks ![]() , each of size
, each of size ![]() , with
, with ![]() , then
, then
![]()
Again, symbolically we apply the same rules as for the scalar product — except that now the result is a matrix.
Example: Gram matrix.
Finally, we can consider so-called outer products. Assume matrix ![]() is partitioned row-wise and matrix
is partitioned row-wise and matrix ![]() is partitioned column-wise. Therefore, we have:
is partitioned column-wise. Therefore, we have:
![]()
The dimensions of these matrices should be consistent such that ![]() are of dimensions
are of dimensions ![]() and
and ![]() respectively and
respectively and ![]() are of dimensions
are of dimensions ![]() and
and ![]() respectively. The dimensions of the resultant matrices
respectively. The dimensions of the resultant matrices ![]() will be
will be ![]() respectively.
respectively.
Then the product ![]() can be expressed in terms of the blocks, as follows:
can be expressed in terms of the blocks, as follows:
![]()
10.4. Trace, scalar product
Trace
The trace of a square ![]() matrix
matrix ![]() , denoted by
, denoted by ![]() , is the sum of its diagonal elements:
, is the sum of its diagonal elements:
![]()
Some important properties:
- Trace of transpose: The trace of a square matrix is equal to that of its transpose.
- Commutativity under trace: for any two matrices
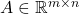 and
and 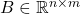 , we have
, we have
![]()
Scalar product between matrices
We can define the scalar product between two ![]() matrices
matrices ![]() via
via
![Rendered by QuickLaTeX.com \[\langle A,B \rangle = {\bf Tr}(A^{T}B) = \sum_{i=1}^{m}\sum_{j=1}^{n}A_{ij}B_{ij}.\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-85d5febb42a8cf8dcd341be71e06049a_l3.png)
The above definition is symmetric: we have
![]()
Our notation is consistent with the definition of the scalar product between two vectors, where we simply view a vector in ![]() as a matrix in
as a matrix in ![]() . We can interpret the matrix scalar product as the vector scalar product between two long vectors of length
. We can interpret the matrix scalar product as the vector scalar product between two long vectors of length ![]() each, obtained by stacking all the columns of
each, obtained by stacking all the columns of ![]() on top of each other.
on top of each other.
![Rendered by QuickLaTeX.com \[ y = x_{1} \begin{pmatrix} A_{11} \\ A_{21} \\ A_{31} \end{pmatrix} + x_{2} \begin{pmatrix} A_{12} \\ A_{22} \\ A_{32} \end{pmatrix}.\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e0166c541c0595a738ccf91c8ffd5028_l3.png)
