Power law model fitting

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

Power law model fitting

Returning to the example involving power laws, we ask the question of finding the ‘‘best’’ model of the form

$\begin{align*} y &= C x_1^{a_1} \cdots x_n^{a_n}, \end{align*}$

given experiments with several input vectors $x_{i}$ and associated outputs $y_i$ , $i=1,\cdots,m$ . Here the variables of our problem are $C$ , and the vector $a \in \mathbb{R}^n$ . Taking logarithms, we obtain

$\begin{align*} \log(y_i) &= \log(C) + a_1 \log(x_{i1}) + \cdots + a_n \log(x_{in}), \end{align*}$

which can be rearranged to the linear form

$\begin{align*} \tilde{y}_i &= a^T \tilde{x}_{i} +b, \quad i=1,\cdots, m, \end{align*}$

where $b = \log(C)$ , and $\tilde{x}_i$ and $\tilde{y}_i$ are the logarithms of $x_i$ and $y_i$ , respectively. We can represent the above linear equations compactly as

$\begin{align*} \begin{pmatrix} \tilde{y}_1 \\ \vdots \\ \tilde{y}_m \end{pmatrix} &= \begin{pmatrix} \tilde{x}_1^T & 1 \\ \vdots & \vdots \\ \tilde{x}_m^T & 1 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix}. \end{align*}$

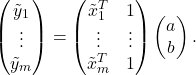
In practice, the power law model is only an approximate representation of reality. Finding the best fit can be formulated as the optimization problem

$\begin{align*} \min\limits_z ||X^Tz-\tilde{y}||_2^2, \end{align*}$

where $z = \begin{pmatrix} a \\ b \end{pmatrix} \in \mathbb{R}^{n+1}$ , $X \in \mathbb{R}^{(n+1) \times m}$ , with the $i$ -th column of $X$ given by $\begin{pmatrix} \tilde{x}_{i} \\ 1 \end{pmatrix}$ , and $\tilde{y} = \begin{pmatrix} \tilde{y}_1 \\ \vdots \\ \tilde{y}_m \end{pmatrix}$ .

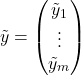See also: Power laws.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

License

Share This Book