Pseudo-inverse of a 4×5 matrix via its SVD

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

Pseudo-inverse of a 4×5 matrix via its SVD

Returning to this example, the pseudo-inverse of the matrix

$\begin{equation*}A = \left( \begin{array}{ccccc} 1 & 0 & 0 & 0 & 2 \\0 & 0 & 3 & 0 & 0 \\0 & 0 & 0 & 0 & 0 \\0 & 4 & 0 & 0 & 0 \end{array} \right).\end{equation*}$

Can be computed via an SVD: $A = U \tilde{S} V^T$ , with

$\begin{align*} U &= \left( \begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 &-1 \\ 1 & 0 & 0 & 0 \end{array} \right) , & \tilde{S} &= \left( \begin{array}{ccccc} 4 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 &\sqrt{5} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right) , & V^T &= \left( \begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \sqrt{0.2} & 0 & 0 & 0 & \sqrt{0.8} \\ 0 & 0 & 0 & 1 & 0 \\ -\sqrt{0.8} & 0 & 0 & 0 &\sqrt{0.2} \end{array} \right) , \end{align*}$

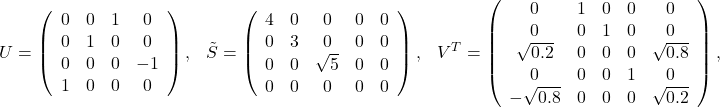
as follows.

We first invert $\tilde{S}$ , simply “inverting what can be inverted” and leaving zero values alone. We get

$\begin{equation*}\tilde{S}^\dagger = \left( \begin{array}{ccccc} 1/4 & 0 & 0 & 0 & 0 \\0 & 1/3 & 0 & 0 & 0 \\0 & 0 &1/\sqrt{5} & 0 & 0 \\0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right).\end{equation*}$

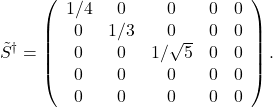
Then the pseudo-inverse is obtained by exchanging the roles of $U$ and $V$ in the SVD:

$\begin{equation*}A^\dagger = V \tilde{S}^\dagger U^T = \left( \begin{array}{ccccc} 0.2000 & 0 & 0 & 0 \\0 & 0 & 0 & 0.2500 \\0 & 0.3333 & 0 & 0 \\0 & 0 & 0 & 0 \\ 0.4000 & 0 & 0 & 0 \end{array} \right).\end{equation*}$

See also: This example.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

License

Share This Book