12 QR DECOMPOSITION OF A MATRIX
12.1 Basic idea
The basic goal of the QR decomposition is to factor a matrix as a product of two matrices (traditionally called ![]() , hence the name of this factorization). Each matrix has a simple structure that can be further exploited in dealing with, say, linear equations.
, hence the name of this factorization). Each matrix has a simple structure that can be further exploited in dealing with, say, linear equations.
The QR decomposition is nothing else than the Gram-Schmidt procedure applied to the columns of the matrix and with the result expressed in matrix form. Consider a ![]() matrix
matrix ![]() , with each
, with each ![]() is a column of
is a column of ![]() .
.
12.2 Case being full column rank
Assume first that ![]() (the columns of
(the columns of ![]() ) are linearly independent. Each step of the G-S procedure can be written as
) are linearly independent. Each step of the G-S procedure can be written as
![]()
We write this as
![]()
where ![]() and
and ![]() .
.
Since the ![]() ‘s are unit-length and normalized, the matrix
‘s are unit-length and normalized, the matrix ![]() satisfies
satisfies ![]() . The QR decomposition of a
. The QR decomposition of a ![]() matrix
matrix ![]() thus allows writing the matrix in factored form:
thus allows writing the matrix in factored form:
![Rendered by QuickLaTeX.com \[ A=Q R, \quad Q=\left(\begin{array}{lll} q_1 & \ldots & q_n \end{array}\right), \quad R=\left(\begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1 n} \\ 0 & r_{22} & & r_{2 n} \\ \vdots & & \ddots & \vdots \\ 0 & & 0 & r_{n n} \end{array}\right) \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c8f393a13c4324081222a121d7ad7fd3_l3.png)
where ![]() is a
is a ![]() matrix with
matrix with ![]() , and
, and ![]() is
is ![]() , upper-triangular.
, upper-triangular.
Example: QR decomposition of a 4×6 matrix.
12.3 Case when the columns are not independent
When the columns of ![]() are not independent, at some step of the G-S procedure we encounter a zero vector
are not independent, at some step of the G-S procedure we encounter a zero vector ![]() , which means
, which means ![]() is a linear combination of
is a linear combination of ![]() . The modified Gram-Schmidt procedure then simply skips to the next vector and continues.
. The modified Gram-Schmidt procedure then simply skips to the next vector and continues.
In matrix form, we obtain ![]() , with
, with ![]() ,
, ![]() , and
, and ![]() has an upper staircase form, for example:
has an upper staircase form, for example:
![Rendered by QuickLaTeX.com \[ R=\left(\begin{array}{cccccc} * & * & * & * & * & *\\ 0 & 0 & * & * & * & * \\ 0 & 0 & 0 & 0 & * & * \end{array}\right). \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-202c198cd31942aa736b95876131f31e_l3.png)
(This is simply an upper triangular matrix with some rows deleted. It is still upper triangular.)
We can permute the columns of ![]() to bring forward the first non-zero elements in each row:
to bring forward the first non-zero elements in each row:
![Rendered by QuickLaTeX.com \[ R=\left( R_1 \mid R_2 \right) P^T,\quad \left( R_1 \mid R_2 \right):=\left(\begin{array}{ccc|ccc} * & * & * & * & * & *\\ 0 & * & 0 & * & * & * \\ 0 & 0 & * & 0 & 0 & * \end{array}\right) \]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f6dbfb2b9af85b394b358d8bb1a047c1_l3.png)
where ![]() is a permutation matrix (that is, its columns are the unit vectors in some order), whose effect is to permute columns. (Since
is a permutation matrix (that is, its columns are the unit vectors in some order), whose effect is to permute columns. (Since ![]() is orthogonal,
is orthogonal, ![]() .) Now,
.) Now, ![]() is square, upper triangular, and invertible, since none of its diagonal elements is zero.
is square, upper triangular, and invertible, since none of its diagonal elements is zero.
The QR decomposition can be written
![]()
where
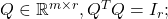
 is the
is the 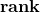 of
of 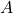 ;
;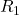 is
is 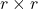 upper triangular, invertible matrix;
upper triangular, invertible matrix;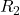 is a
is a 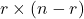 matrix;
matrix;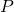 is a
is a 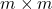 permutation matrix.
permutation matrix.
12.4 Full QR decomposition
The full QR decomposition allows to write ![]() where
where ![]() is square and orthogonal (
is square and orthogonal (![]() ). In other words, the columns of
). In other words, the columns of ![]() are an orthonormal basis for the whole output space
are an orthonormal basis for the whole output space ![]() , not just for the range of
, not just for the range of ![]() .
.
We obtain the full decomposition by appending an ![]() identity matrix to the columns of
identity matrix to the columns of ![]() :
: ![]() . The QR decomposition of the augmented matrix allows to write
. The QR decomposition of the augmented matrix allows to write
![]()
where the columns of the ![]() matrix
matrix ![]() are orthogonal and
are orthogonal and ![]() is upper triangular and invertible. (As before,
is upper triangular and invertible. (As before, ![]() is a permutation matrix.) In the G-S procedure, the columns of
is a permutation matrix.) In the G-S procedure, the columns of ![]() are obtained from those of
are obtained from those of ![]() , while the columns of
, while the columns of ![]() come from the extra columns added to
come from the extra columns added to ![]() .
.
The full QR decomposition reveals the rank of ![]() : we simply look at the elements on the diagonal of
: we simply look at the elements on the diagonal of ![]() that are not zero, that is, the size of
that are not zero, that is, the size of ![]() .
.
Example: QR decomposition of a 4×6 matrix.
