"

Quadratic functions in two variables

Two examples of quadratic functions are p,q: \mathbb{R}^2 \rightarrow \mathbb{R}, with values

    \begin{align*} p(x) &= 4x_1^2 + 2x_2^2 + 3x_1 x_2 +4x_1 + 5x_2 + 2\times 10^5 \end{align*}

    \begin{align*} q(x) &= 4x_1^2 - 2x_2^2 + 3x_1 x_2 +4x_1 + 5x_2 + 2\times 10^5 \end{align*}

The function

    \begin{align*} r(x) &= 4x_1^2 + 2x_2^2 + 3x_1 x_2 \end{align*}

is a form, since it has no linear or constant terms in it.

 

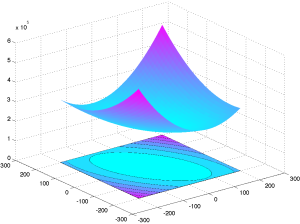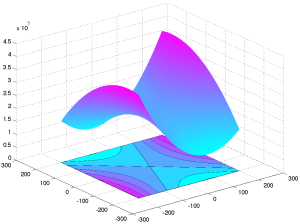Level sets and graph of the quadratic function p. The epigraph is anything that extends above the graph in the z-axis direction. This function is ‘‘bowl-shaped’’, or convex.
 

Level sets and graph of the quadratic function q. This quadratic function is not convex.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Linear Algebra and Applications Copyright © 2023 by VinUiversity is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book