Rank-one matrices: A representation theorem

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

Rank-one matrices: A representation theorem

We prove the theorem mentioned here:

Theorem: outer product representation of a rank-one matrix

Every rank-one matrix $A \in \mathbb{R}^{m \times n}$ can be written as an ‘‘outer product’’, or dyad:

$A = pq^T,$

where $p \in \mathbb{R}^{m}, \; q \in \mathbb{R}^{n}$ .

Proof: For any non-zero vectors $p \in \mathbb{R}^{m}, q \in \mathbb{R}^{n}$ , the matrix $pq^T$ is indeed of rank one: if $x \in \mathbb{R}^{n}$ , then

$pq^Tx=(q^Tx)p.$

When $x$ spans $\mathbb{R}^{n}$ , the scalar $q^Tx$ spans the entire real line (since $q \neq 0$ ), and the vector $(q^Tx)p$ spans the subspace of vectors proportional to $p$ . Hence, the range of $pq^T$ is the line:

$\mathbf{R}(pq^T) = \{tp\; : \;t \in \mathbb{R}\},$

which is of dimension 1.

Conversely, if $A$ is of rank one, then its range is of dimension one, hence it must be a line passing through $0$ . Hence for any $x$ there exist a function $t: \mathbb{R} \rightarrow \mathbb{R}$ such that

$Ax = t(x)p.$

Using $x = e_i$ , where $e_i$ is the $i-$ th vector of the standard basis, we obtain that there exist numbers $t_1, ... t_n$ such that for every $i$ :

$Ae_i = t_ip, \quad i=1,...,n.$

We can write the above in a single matrix equation:

$A \begin{pmatrix} e_1 & \cdots & e_n \end{pmatrix} = p \begin{pmatrix} t_1 & \cdots & t_n \end{pmatrix}$

Now letting 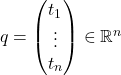$q = \begin{pmatrix} t_1 \\ \vdots \\ t_n \end{pmatrix} \in \mathbb{R}^{n}$ and realizing that the matrix $(e_1, ..., e_n)$ is simply the identity matrix, we obtain $A = pq^T$ , as desired.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Theorem: outer product representation of a rank-one matrix

License

Share This Book