Rate of return of a financial portfolio

Rate of return of a single asset

The rate of return r (or the return) of a financial asset over a given period (say, a year, or a day) is the interest obtained at the end of the period by investing in it. In other words, if, at the beginning of the period, we invest a sum S in the asset, we will earn S_{\text{end}}:=(1+r)S at the end. That is:

    \begin{align*} r &= \frac{S_{\text{end}} - S}{S}. \end{align*}

Log-returns

Often, the rates of return are approximated, especially if the period length is small. If r \ll 1, then

    \begin{align*} r &= \frac{S_{\text{end}}}{S} - 1 \approx y := \log\left(\frac{S_{\text{end}}}{S}\right), \end{align*}

with the latter quantity known as log-return.

Rate of return of a portfolio

For n assets, we can define the vector r \in \mathbb{R}^n, with r_i the rate of return of the i-th asset.

Assume that at the beginning of the period, we invest a sum S in all the assets, allocating a fraction x_i (in \%) in the i-th asset. Here x \in \mathbb{R}^n is a non-negative vector which sums to one. Then the portfolio we constituted this way will earn

    \begin{align*} S_{\text{end}} &= \sum\limits_{i=1}^{n} (1 + r_i)x_iS. \end{align*}

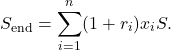
The rate of return of the porfolio is the relative increase in wealth:

    \begin{align*} \frac{S_{\text{end}} - S}{S} &= \sum\limits_{i=1}^n (1 + r_i)x_i - 1 = \sum\limits_{i=1}^n x_i - 1 + \sum\limits_{i=1}^n r_i x_i = r^T x. \end{align*}

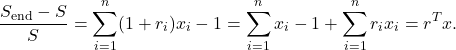
The rate of return is thus the scalar product between the vector of individual returns r and of the portfolio allocation weights x.

Note that, in practice, rates of return are never known in advance, and they can be negative (although, by construction, they are never less than -1).

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Linear Algebra and Applications Copyright © 2023 by VinUiversity is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book