Sample covariance matrix
Definition
For a vector ![]() , the sample variance
, the sample variance ![]() measures the average deviation of its coefficients around the sample average
measures the average deviation of its coefficients around the sample average ![]() :
:
![]()
Now consider a matrix ![]() , where each column
, where each column ![]() represents a data point in
represents a data point in ![]() . We are interested in describing the amount of variance in this data set. To this end, we look at the numbers we obtain by projecting the data along a line defined by the direction
. We are interested in describing the amount of variance in this data set. To this end, we look at the numbers we obtain by projecting the data along a line defined by the direction ![]() . This corresponds to the vector in
. This corresponds to the vector in ![]() .
.
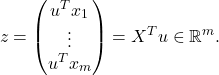
The corresponding sample mean and variance are
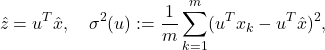
where ![]() is the sample mean of the vectors [latex]x_1, \cdots, x_m[/latex].
is the sample mean of the vectors [latex]x_1, \cdots, x_m[/latex].
The sample variance along direction ![]() can be expressed as a quadratic form in
can be expressed as a quadratic form in ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*} \sigma^2(u) &= \frac{1}{m} \sum_{k=1}^m [u^T(x_k-\hat{x})]^2 = u^T\Sigma u, \end{align*}](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5a56ecb15e6a4b21deb124a76dc59229_l3.png)
where ![]() is a
is a ![]() symmetric matrix, called the sample covariance matrix of the data points:
symmetric matrix, called the sample covariance matrix of the data points:
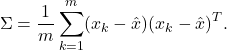
Properties
The covariance matrix satisfies the following properties:
- The sample covariance matrix allows finding the variance along any direction in data space.
- The diagonal elements of
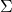 give the variances of each vector in the data.
give the variances of each vector in the data. - The trace of
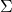 gives the sum of all the variances.
gives the sum of all the variances. - The matrix
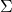 is positive semi-definite, since the associated quadratic form
is positive semi-definite, since the associated quadratic form 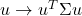 is non-negative everywhere.
is non-negative everywhere.
