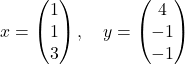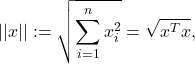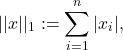2 SCALAR PRODUCT, NORMS AND ANGLES
2.1. Scalar product
Definition
The scalar product (or, inner product, or dot product) between two vectors ![]() is the scalar denoted
is the scalar denoted ![]() , and defined as
, and defined as
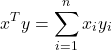
The motivation for our notation above will come later when we define the matrix-matrix product. The scalar product is also sometimes denoted ![]() , a notation that originates in physics.
, a notation that originates in physics.
See also:
- Rate of return of a financial portfolio.
- Sample and weighted average.
- Beer-Lambert law in absorption spectroscopy.
Orthogonality
We say that two vectors ![]() are orthogonal if
are orthogonal if ![]() .
.
| Example 1: The two vectors in |
|
|
| are orthogonal, since |
|
|
2.2. Norms
Definition
Measuring the size of a scalar value is unambiguous — we just take the magnitude (absolute value) of the number. However, when we deal with higher dimensions and try to define the notion of size, or length, of a vector, we are faced with many possible choices. These choices are encapsulated in the notion of norm.
Norms are real-valued functions that satisfy a basic set of rules that a sensible notion of size should involve. You can consult the formal definition of a norm here. The norm of a vector ![]() is usually denoted
is usually denoted ![]()
2.3. Three popular norms
In this course, we focus on the following three popular norms for a vector ![]() :
:
| The |
|
|
|
|
| corresponds to the distance traveled on a rectangular grid to go from one point to another. | |
| The |
|
|
|
|
| is useful in measuring peak values. | |
Examples:
- A given vector will in general have different ‘‘lengths” under different norms. For example, the vector
![Rendered by QuickLaTeX.com x = [1, -2, 3]^T](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-adc114843e0b78439d7859deec9fb606_l3.png) yields
yields 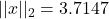 ,
, 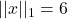 , and
, and 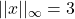 .
. - Sample standard deviation.
2.4. Cauchy-Schwarz inequality
The Cauchy-Schwarz inequality allows to bound the scalar product of two vectors in terms of their Euclidean norm.
Theorem: Cauchy-Schwarz inequality
|
For any two vectors
The above inequality is an equality if and only if
with optimal |
2.5. Angles between vectors
When none of the vectors ![]() is zero, we can define the corresponding angle as
is zero, we can define the corresponding angle as ![]() such that
such that
![]()
Applying the Cauchy-Schwartz inequality above to ![]() and
and ![]() we see that indeed the number above is in
we see that indeed the number above is in ![]() .
.
The notion above generalizes the usual notion of angle between two directions in two dimensions, and is useful in measuring the similarity (or, closeness) between two vectors. When the two vectors are orthogonal, that is, ![]() , we do obtain that their angle is
, we do obtain that their angle is ![]() .
.
See also: Similarity of two documents.