Single factor model of financial price data
Consider a ![]() data matrix which contains the log-returns of
data matrix which contains the log-returns of ![]() assets over
assets over ![]() time periods (say, days).
time periods (say, days).
A single-factor model for this data is one based on the assumption that the matrix is a dyad:
![]()
where ![]() , and
, and ![]() . In practice, no component of
. In practice, no component of ![]() and
and ![]() is zero (if that is not the case, then a whole row or column of
is zero (if that is not the case, then a whole row or column of ![]() is zero and can be ignored in the analysis).
is zero and can be ignored in the analysis).
According to the single factor model, the entire market behaves as follows. At any time ![]() , the log-return of asset
, the log-return of asset ![]() is of the form
is of the form ![]() .
.
The vectors ![]() and
and ![]() have the following interpretation.
have the following interpretation.
- For any asset, the rate of change in log-returns between two-time instants
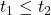 is given by the ratio
is given by the ratio 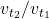 , independent of the asset. Hence,
, independent of the asset. Hence,  gives the time profile for all the assets: every asset shows the same time profile, up to a scaling given by
gives the time profile for all the assets: every asset shows the same time profile, up to a scaling given by 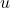 .
. - Likewise, for any time
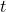 , the ratio between the log-returns of two assets
, the ratio between the log-returns of two assets 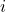 and
and 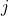 at time
at time 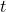 is given by
is given by 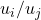 , independent of
, independent of 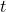 . Hence
. Hence 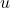 gives the asset profile for all the time periods. Each time shows the same asset profile, up to a scaling given by
gives the asset profile for all the time periods. Each time shows the same asset profile, up to a scaling given by  .
.
While single-factor models may seem crude, they often offer a reasonable amount of information. It turns out that with many financial market data, a good single factor model involves a time profile  equal to the log-returns of the average of all the assets, or some weighted average (such as the SP 500 index). With this model, all assets follow the profile of the entire market.
equal to the log-returns of the average of all the assets, or some weighted average (such as the SP 500 index). With this model, all assets follow the profile of the entire market.
