20 SOLVING LINEAR EQUATIONS VIA QR DECOMPOSITION
20.1. Basic idea: reduction to triangular systems of equations
Consider the problem of solving a system of linear equations ![]() , where
, where ![]() and
and ![]() are given.
are given.
The basic idea in the solution algorithm starts with the observation that in the special case when ![]() is upper triangular, that is,
is upper triangular, that is, ![]() if
if ![]() , then the system can be easily solved by a process known as backward substitution. In backward substitution we simply start solving the system by eliminating the last variable first, then proceed to solve backwards. The process is illustrated in this example, and described in generality here.
, then the system can be easily solved by a process known as backward substitution. In backward substitution we simply start solving the system by eliminating the last variable first, then proceed to solve backwards. The process is illustrated in this example, and described in generality here.
20.2. The QR decomposition of a matrix
The QR decomposition allows to express any ![]() matrix
matrix ![]() as the product
as the product ![]() where
where ![]() is
is ![]() and orthogonal (that is,
and orthogonal (that is, ![]() ) and
) and ![]() is an
is an ![]() upper triangular. For more details on this, see here.
upper triangular. For more details on this, see here.
Once the QR factorization of ![]() is obtained, we can solve the system by first pre-multiplying with
is obtained, we can solve the system by first pre-multiplying with ![]() both sides of the equation:
both sides of the equation:
![]()
This is due to the fact that ![]() . The new system
. The new system ![]() is triangular and can be solved by backwards substitution. For example, if
is triangular and can be solved by backwards substitution. For example, if ![]() is full column rank, then
is full column rank, then ![]() is invertible, so that the solution is unique, and given by
is invertible, so that the solution is unique, and given by ![]() .
.
Let us detail the process now.
20.3. Using the full QR decomposition
We start with the full QR decomposition of A with column permutations:
![]()
where
![Rendered by QuickLaTeX.com Q = [Q_1, Q_2]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3499b5c65af625226d990350ecae54d0_l3.png) is
is 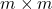 and orthogonal (
and orthogonal (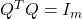 );
);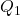 is
is 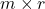 , with orthonormal columns (
, with orthonormal columns (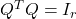 );
);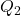 is
is 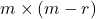 , with orthonormal columns (
, with orthonormal columns (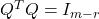 );
); is the rank of
is the rank of 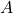 ;
;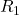 is
is 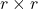 upper triangular, and invertible;
upper triangular, and invertible;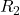 is a
is a 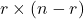 matrix;
matrix;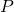 is a
is a 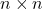 permutation matrix (thus,
permutation matrix (thus, 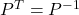 ).
).- The zero submatrices in the bottom (block) row of
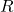 have
have 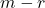 rows.
rows.
Using ![]() , we can write
, we can write ![]() , where
, where ![]() . Let’s look at the equation in
. Let’s look at the equation in ![]() in expanded form:
in expanded form:
![]()
We see that unless ![]() , there is no solution. Let us assume that
, there is no solution. Let us assume that ![]() . We have then
. We have then
![]()
which is a set of ![]() linear equations in
linear equations in ![]() variables.
variables.
A particular solution is obtained upon setting ![]() , which leads to a triangular system in
, which leads to a triangular system in ![]() , with an invertible triangular matrix
, with an invertible triangular matrix ![]() . So that
. So that ![]() , which corresponds to a particular solution
, which corresponds to a particular solution ![]() to
to ![]() :
:
![]()
20.4. Set of solutions
We can also generate all the solutions, by noting that ![]() is a free variable. We have
is a free variable. We have
![]()
where
![]()
The set of solutions is the affine set
![]()
