SOLVING LINEAR SYSTEMS VIA SVD

Alicia Y. Tsai; Authors: Laurent EI Ghaoui; Contributors: Phan Hoang, Tony Tin, Ha To Tam, Nguyen Van Kep, Le Dinh Nam, Juliette Decugis, Nguyen Quoc Cuong.; Giuseppe C. Calafiore

36 SOLVING LINEAR SYSTEMS VIA SVD

36.1. Solution set

Consider a linear equation

$Ax = y,$

where $A \in \mathbb{R}^{m\times n}$ and $y \in \mathbb{R}^m$ are given. We can completely describe the set of solutions via SVD, as follows. Let us assume that $A$ admits an SVD given here. With $A = U\tilde{S}V^T$ pre-multiply the linear equation by the inverse of $U$ , $U^T$ ; then we express the equation in terms of the rotated vector $\tilde{x} = V^Tx$ . This leads to

$\tilde{S}\tilde{x}=\tilde{y},$

where $\tilde{y} := U^Ty$ is the “rotated” right-hand side of the equation.

Due to the simple form of $\tilde{S}$ , the above writes

$\begin{aligned} \sigma_i \tilde{x}_i &= \tilde{y}_i, & i &= 1, \ldots, r, \\ 0 &= \tilde{y}_i, & i &= r+1, \ldots, m. \end{aligned}$

Two cases can occur:

If the last 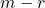$m-r$ components of 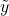$\tilde{y}$ are not zero, then the above system is infeasible, and the solution set is empty. This occurs when 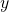$y$ is not in the range of $A$ .
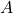If 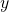$y$ is in the range of 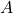$A$ , then the last set of conditions in the above system hold, and we can solve for 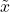$\tilde{x}$ with the first set of conditions:

$\tilde{x}_i = \frac{\tilde{y}_i}{\sigma_i}, \quad i = 1,\ldots, r.$

The last $n-r$ components of $\tilde{x}$ are free. This corresponds to elements in the nullspace of $A$ . If $A$ is full column rank (its nullspace is reduced to { $0$ }, then there is a unique solution.

36.2. Pseudo-inverse

Definition

The solution set is conveniently described in terms of the pseudo-inverse of $A$ , denoted by $A^\dagger$ , and defined via the SVD of $A$ :

$A = U \tilde{S} V^T, \quad \tilde{S} = \textbf{diag}(\sigma_1,\ldots,\sigma_r,0,\ldots,0),$

as one with the same SVD, with non-zero singular values inverted, and the matrix $\tilde{S}$ transposed:

$A^\dagger := V \tilde{S}^\dagger U^T, \quad \tilde{S} = \textbf{diag}(\sigma_1^{-1},\ldots,\sigma_r^{-1},0,\ldots,0).$

The pseudo-inverse of a matrix is always well-defined, and it has the same size as the transpose $A^T$ . When the matrix is invertible (it is square and full column or row rank: $m=n=r$ ), then it reduces to the inverse.

Example: pseudo-inverse of a $4 \times 5$ matrix.

Link with solution set

From the above development, we see that the solution set can be written as

$\mathbf{S} = \left\{ A^\dagger y + z :~ z \in \mathbf{N}(A) \right\},$

where $\mathbf{N}(A)$ is the nullspace of $A$ . Both $A^\dagger$ and a basis for the nullspace can be computed via the SVD.

Case when 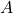$A$ is full rank

If $A$ is full column rank, the pseudo-inverse can be written as

$A^\dagger = (A^T A)^{-1} A^T.$

In that case, $A^\dagger$ is a left-inverse of $A$ , since $A^\dagger A = I_n$ .

If $A$ is full row-rank, then the pseudo-inverse can be written as

$A^\dagger = A^T (A A^T)^{-1}.$

In that case, $A^\dagger$ is a right-inverse of $A$ , since $A A^\dagger = I_m$ .

36.3. Sensitivity analysis and condition number

Sensitivity analysis refers to the process of quantifying the impact of changes in the linear equations’ coefficients (the matrix $A$ and vector $y$ ) on the solution. To simplify, let us assume that $A$ is square and invertible, and analyze the effects of errors in $y$ only. The condition number of the matrix $A$ quantifies this.

We start from the linear equation above, which has the unique solution $x = A^{-1} y$ . Now assume that $y$ is changed into $y + \delta y$ , where $\delta y$ is a vector that contains the changes in $y$ . Let’s denote by $x + \delta x$ the new solution, which is $A^{-1} (y + \delta y)$ . From the equations:

$\delta x = A^{-1} \delta y,$

and using the definition of the largest singular value norm, we obtain:

$\|\delta x\|_2 \leq \|A^{-1}\| \cdot \|\delta y\|_2, \quad \|y\|_2 \leq \|A\| \cdot \|x\|_2.$

Combining the two inequalities we get:

$\frac{\|\delta x\|_2}{\|x\|_2} \leq \kappa(A) \cdot \frac{\|\delta y\|_2}{\|y\|_2},$

where $\kappa(A)$ is the condition number of $A$ , defined as:

$\kappa(A) := \|A\| \cdot \|A^{-1}\|.$

We can express the condition number as the ratio between the largest and smallest singular values of $A$ :

$\kappa(A) = \frac{\sigma_1(A)}{\sigma_n(A)}.$

The condition number gives a bound on the ratio between the relative error in the left-hand side to that of the solution. We can also analyze the effect of errors in the matrix itself on the solution. The condition number turns out to play a crucial role there as well.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License