Standard forms
Functional form
An optimization problem is a problem of the form
![]()
where
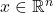 is the decision variable;
is the decision variable;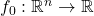 is the objective function, or cost;
is the objective function, or cost;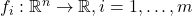 represent the constraints;
represent the constraints;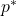 is the optimal value.
is the optimal value.
In the above, the term ‘‘subject to’’ is sometimes replaced with the shorthand colon notation.
Often the above is referred to as a ‘‘mathematical program’’. The term “programming” (or “program”) does not refer to a computer code. It is used mainly for historical purposes. We will use the more rigorous (but less popular) term “optimization problem”.
Example: An optimization problem in two variables.
Epigraph form
In optimization, we can always assume that the objective is a linear function of the variables. This can be done via the epigraph representation of the problem, which is based on adding a new scalar variable ![]() :
:
![]()
At optimum, ![]() . In the above, the objective function is
. In the above, the objective function is ![]() , with values
, with values ![]() .
.
We can picture this as follows. Consider the sub-level sets of the objective function, which are of the form ![]() for some
for some ![]() . The problem amounts to finding the smallest
. The problem amounts to finding the smallest ![]() for which the corresponding sub-level set intersects the set of points that satisfy the constraints.
for which the corresponding sub-level set intersects the set of points that satisfy the constraints.
Example: Geometric view of the optimization problem in two variables.
Other standard forms
Sometimes we single out equality constraints, if any:
![]()
where ![]() ‘s are given. Of course, we may reduce the above problem to the standard form above, representing each equality constraint by a pair of inequalities.
‘s are given. Of course, we may reduce the above problem to the standard form above, representing each equality constraint by a pair of inequalities.
Sometimes, the constraints are described abstractly via a set condition, of the form ![]() for some subset
for some subset ![]() of
of ![]() . The corresponding notation is
. The corresponding notation is
![]()
Some problems come in the form of maximization problems. Such problems are readily cast in standard form via the expression
![]()
where ![]() .
.
