SVD: A 4×4 example
Consider a matrix ![]() in
in ![]() , with SVD given by
, with SVD given by
![]()
where
![]()
From the SVD, we can understand the behavior of the mapping ![]() :
:
- Input components along directions corresponding to
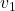 and
and 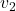 are amplified (by factors of 10 and 7, respectively) and come out mostly along the plane spanned by
are amplified (by factors of 10 and 7, respectively) and come out mostly along the plane spanned by 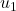 and
and 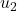 .
. - Input components along directions corresponding to
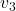 and
and 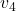 are attenuated (by factors of 0.1 and 0.05, respectively).
are attenuated (by factors of 0.1 and 0.05, respectively). - The matrix
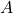 is nonsingular.
is nonsingular. - For some applications, it might be appropriate to consider
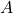 as effectively rank 2, given the significant attenuation for components along
as effectively rank 2, given the significant attenuation for components along 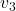 and
and 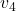 .
.
