34 THE SVD THEOREM
34.1. The SVD theorem
Basic idea
Recall from here that any matrix ![]() with rank one can be written as
with rank one can be written as
![]()
where ![]() , and
, and ![]() .
.
It turns out that a similar result holds for matrices of arbitrary rank ![]() . That is, we can express any matrix
. That is, we can express any matrix ![]() of rank
of rank ![]() as sum of rank-one matrices
as sum of rank-one matrices
![]()
where ![]() are mutually orthogonal,
are mutually orthogonal, ![]() are also mutually orthogonal, and the
are also mutually orthogonal, and the ![]() ‘s are positive numbers called the singular values of
‘s are positive numbers called the singular values of ![]() . In the above,
. In the above, ![]() turns out to be the rank of
turns out to be the rank of ![]() .
.
Theorem statement
The following important result applies to any matrix ![]() , and allows us to understand the structure of the mapping
, and allows us to understand the structure of the mapping ![]() .
.
Theorem: Singular Value Decomposition (SVD)
|
An arbitrary matrix
where
where the positive numbers
|
This proof of the theorem hinges on the spectral theorem for symmetric matrices. Note that in the theorem, the zeros appearing alongside ![]() represents blocks of zeros. They may be empty, for example if
represents blocks of zeros. They may be empty, for example if ![]() then there are no zeros to the right of
then there are no zeros to the right of ![]() .
.
Computing the SVD
The SVD of an ![]() matrix
matrix ![]() can be computed via a sequence of linear transformations. The computational complexity of the algorithm, when expressed in terms of the number of floating-point operations, is given by
can be computed via a sequence of linear transformations. The computational complexity of the algorithm, when expressed in terms of the number of floating-point operations, is given by
![]()
This complexity can become substantial when dealing with large, dense matrices. However, for sparse matrices, one can expedite the computation if only the largest few singular values and their corresponding singular vectors are of interest. To understand the derivation of this complexity:
- The outer product of vectors
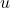 and
and 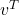 has a complexity of
has a complexity of 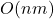 . This is because for a vector
. This is because for a vector 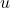 of length
of length 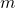 and a vector
and a vector  of length
of length 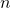 , the outer product results in an
, the outer product results in an 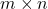 matrix, and computing each entry requires one multiplication.
matrix, and computing each entry requires one multiplication. - The matrix
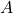 has at most
has at most  non-zero singular values, where
non-zero singular values, where 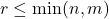 . Each of these singular values will contribute to the overall computational cost.
. Each of these singular values will contribute to the overall computational cost. - Combining the costs from the two previous steps, the total computational complexity becomes
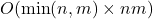 .
.
Example: A ![]() example.
example.
34.2. Geometry
The theorem allows to decompose the action of ![]() on a given input vector as a three-step process. To get
on a given input vector as a three-step process. To get ![]() , where
, where ![]() , we first form
, we first form ![]() . Since
. Since ![]() is an orthogonal matrix,
is an orthogonal matrix, ![]() is also orthogonal, and
is also orthogonal, and ![]() is just a rotated version of
is just a rotated version of ![]() , which still lies in the input space. Then we act on the rotated vector
, which still lies in the input space. Then we act on the rotated vector ![]() by scaling its elements. Precisely, the first
by scaling its elements. Precisely, the first ![]() elements of
elements of ![]() are scaled by the singular values
are scaled by the singular values ![]() ; the remaining
; the remaining ![]() elements are set to zero. This step results in a new vector
elements are set to zero. This step results in a new vector ![]() which now belongs to the output space
which now belongs to the output space ![]() . The final step consists in rotating the vector
. The final step consists in rotating the vector ![]() by the orthogonal matrix
by the orthogonal matrix ![]() , which results in
, which results in ![]() .
.
For example, assume ![]() has the simple form
has the simple form
![Rendered by QuickLaTeX.com \[A = \begin{pmatrix} 1.3 & 0 \\ 0 & 2.1 \\ 0 & 0 \end{pmatrix},\]](https://pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0eb65ccaff966543c8af6d5ebd87021e_l3.png)
then for an input vector ![]() in
in ![]() ,
, ![]() is a vector in
is a vector in ![]() with first component
with first component ![]() , second component
, second component ![]() , and last component being zero.
, and last component being zero.
To summarize, the SVD theorem states that any matrix-vector multiplication can be decomposed as a sequence of three elementary transformations: a rotation in the input space, a scaling that goes from the input space to the output space, and a rotation in the output space. In contrast with symmetric matrices, input and output directions are different.
The interpretation allows to make a few statements about the matrix.
Example: A ![]() example.
example.
34.3. Link with the SED (Spectral Theorem)
If ![]() admits an SVD, then the matrices
admits an SVD, then the matrices ![]() and
and ![]() has the following SEDs:
has the following SEDs:
![]()
where
![]()
is ![]() (so it has
(so it has ![]() trailing zeros), and
trailing zeros), and
![]()
is ![]() (so it has
(so it has ![]() trailing zeros). The eigenvalues of
trailing zeros). The eigenvalues of ![]() and
and ![]() are the same, and equal to the squared singular values of
are the same, and equal to the squared singular values of ![]() .
.
The corresponding eigenvectors are the left and right singular vectors of ![]() .
.
This is a method (not the most computationally efficient) to find the SVD of a matrix, based on the SED.
