LEAST-SQUARES
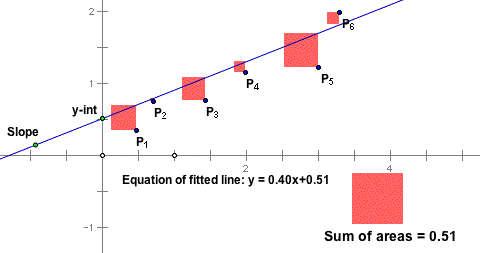
The ordinary least-squares (OLS) problem is a particularly simple optimization problem that involves the minimization of the Euclidean norm of a ‘‘residual error” vector that is affine in the decision variables. The problem is one of the most ubiquituous optimization problems in engineering and applied sciences. It can be used for example to fit a straight line through points, as in the figure on the left. The least-squares approach then amounts to minimize the sum of the area of the squares with side-length equal to the vertical distances to the line.
We discuss a few variants amenable to the linear algebra approach: regularized least-squares, linearly-constrained least-squares. We also explain how to use ‘‘kernels’’ to handle problems involving non-linear curve fitting and prediction using non-linear functions.