33 Principle of superposition

Interference and the principle of superposition

Unlike particles, waves can and do pass through each other. After the waves meet, they return to their original “selves” and continue on as if they had never interacted at all.

Where and when waves overlap, the waves combine to form a single wave. This phenomenon is called interference. The basic rule that governs interference is the principle of superposition:

Where two (or more) waves (or pulses) overlap, the displacements of the resulting wave (or pulse) is equal to the sum of the displacements each wave (or pulse) would have if it was at the location alone.

If two crests (or two troughs) line up, the result is a pulse/wave that’s larger than either crest (trough) alone- this is called constructive interference.

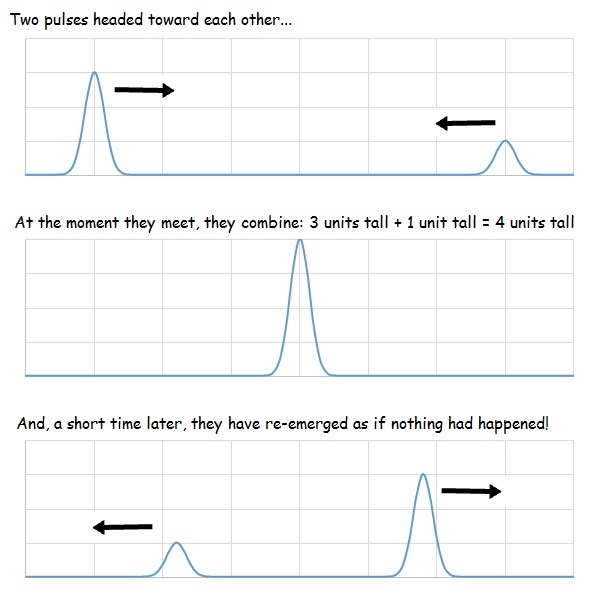
If crest meets trough, the result is a smaller pulse/wave- this is called destructive interference. Notice that the interference only occurs while the two waves overlap. Once the waves/pulses travel pass each other, they reemerge as if nothing had happened!

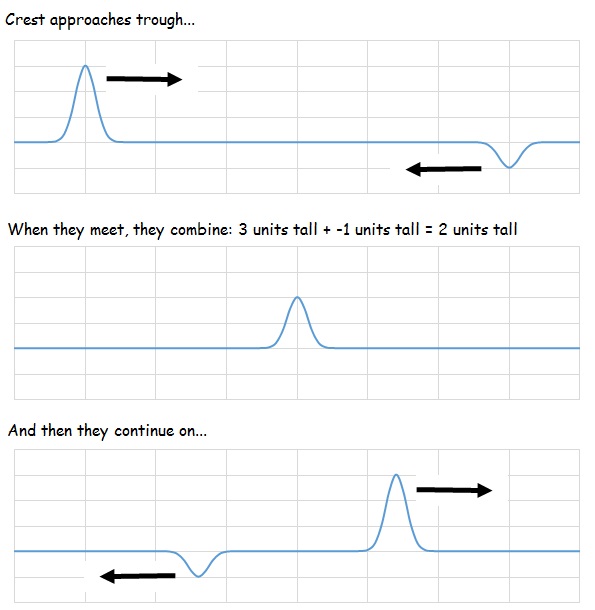
No matter whether it’s constructive or destructive interference, the math is addition. At the exact moment a pulse with a crest 3 units tall meets meets pulse with a crest 1 unit tall, the pulse is temporarily 4 units tall. When a crest 3 units tall meets meets a trough 1 unit deep, the pulse is 2 units tall. (Think of troughs as having negative height).

A closer look at the math

At the exact moment a crest 3 units tall perfectly aligns a crest 1 unit tall, the result is a crest that’s 4 units tall. But what happens when if the two pulses don’t align perfectly? Intuition suggests the result won’t be a single peak- the combined shape will probably retain some of the features of the two individual pulses but the combined shape will be taller that either pulse alone. Intuition also suggests that  exact answer depends on the shapes of the two pulses and how they line up. Does the principle of superposition still apply? The short answer is “yes.” This popsicle sticks video (0:39 youTube) ^[1] shows how.

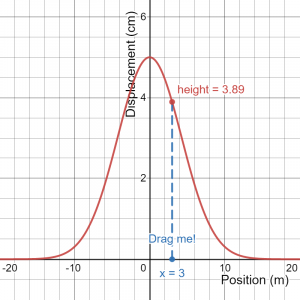
The key insight is recognizing that pulses/waves cannot be described by a single number for height. At each location in the medium, the pulse/wave has a different “height.” In math-speak, displacement is a function of position. Displacement refers to the “height” of the wave above the x-axis and position refers to the location in the medium where you measured the displacement. In the figure below, the displacement is 3.89 cm at position x=3 meters. (Explore how displacement varies with the interactive version of the graph).

Every location in a wave/pulse has a different displacement. So does the shape that results when two pulses/waves overlap. At every location in the medium, the displacements of the two individual waves/pulses add together to form the medium’s displacement at that location. This static figure below shows the basics. For more detail, check out the interactive version of this figure which allows you to move the pulses and the vertical line.

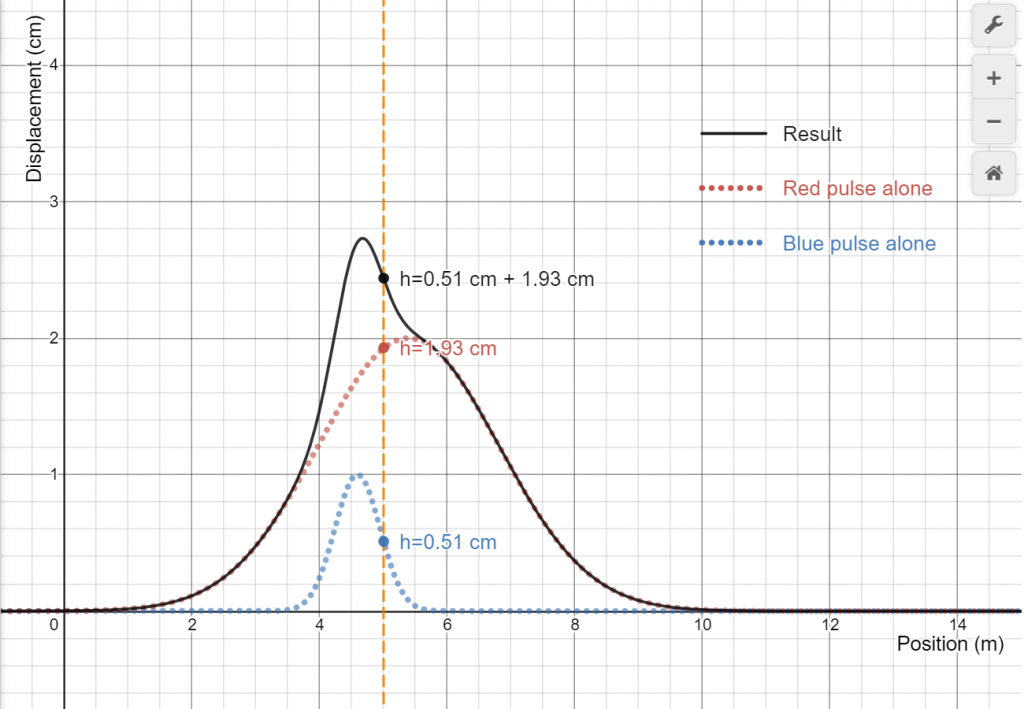
The vertical line shows how the addition works at a single location in the medium. In principle, applying the principle of superposition to find how two pulses add means doing an infinite number of additions- one for every location in the medium. In practice, there are lots of shortcuts that make the job easier.

The figure below shows an example. The upper panel shows a snapshot showing two pulses as if each were alone on a slinky. What will the slinky look like at this moment? (Try not to peek at the answer below). The answer can be worked out by applying the superposition principle at just four key locations in the medium (shown by the arrows in the figure) where changes occur. Adding the displacements of the two pulses at these four locations shows the displacement of the slinky at these four locations. You can fill in the gaps by connecting the dots to reveal the overall shape. You can check your answer easily. The displacements must add correctly at every location in the medium (such as at [latex]x=2 \:m[/latex] or  [latex]x=4 \:m[/latex])- not just the four locations used to figure out the answer.

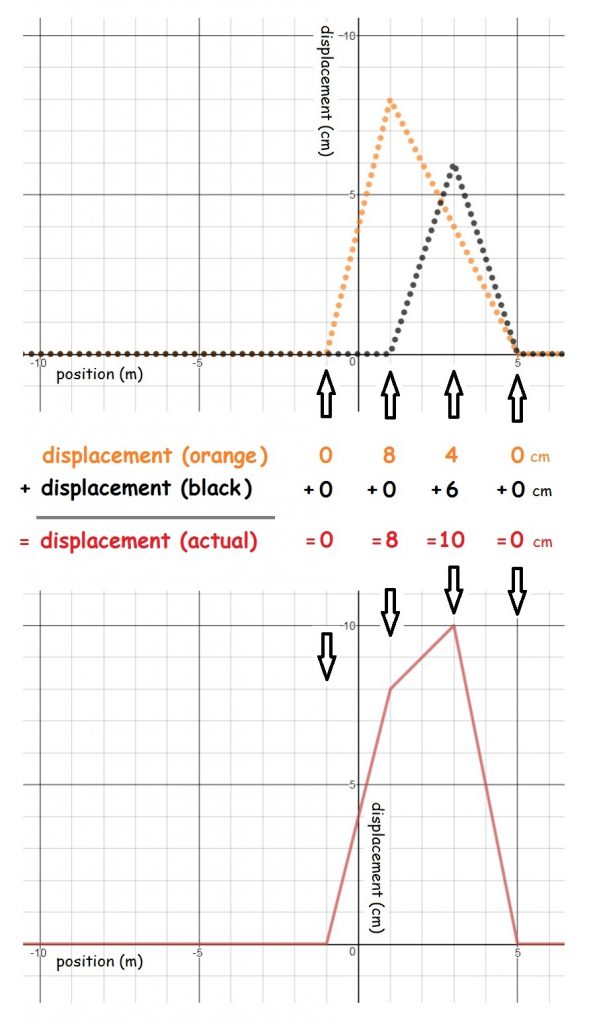
The example shows how superposition works at one instant in time. The youTube video SuperpositionDesmos (3:36) ^[2] shows another worked out example similar to the one above. Superposition of waves (an 0:08 youtube posted by physics007animations) ^[3] shows that how the superposition principle applies to moving pulses. Pause the video at any moment, and you’ll notice that principle of superposition holds for every location along the x-axis.

Solving problems with the superposition principle

The examples above reveal an important facet of the superposition principle- it applies at every location in the medium and at all moments in time. Simply put, superposition applies everywhere and always. In principle, you can solve every superposition and interference problem by following a simple recipe:

1. Figure out where each pulse/wave would be (if it were alone in the medium) at a particular moment in time
2. Add up the displacements for all the pulses/waves at some location in the medium.
3. Repeat step 2 for every single location in the medium.
4. Repeat steps 1 through 3 for every moment in time.

In reality, the process above is impossibly tedious. You have to find shortcuts, learn more math or get computers involved to solve real world problems. The simplest strategy is to apply the superposition principle only at a few carefully chosen locations and times and fill in the rest. In the example above, you can figure out the overall shape considering only the locations where important changes occur: [latex]x=-1 \:meters[/latex], [latex]x=1 \:meters[/latex], [latex]x=3 \:meters[/latex] and [latex]x=5 \:meters[/latex]. You fill in the rest by “connecting the dots.”

Image credits

All images created by Abbott using desmos.com