Musical instruments
29 Helmholtz resonators
Wine bottles
If you’ve ever blown across a wine bottle or pop bottle, you’ve heard a pitch- clear evidence of resonance. If you try to use the open/closed air column model shown in the last section to predict the pitch the bottle will make, you will be pretty far off. What’s wrong?
Helmholtz Resonators
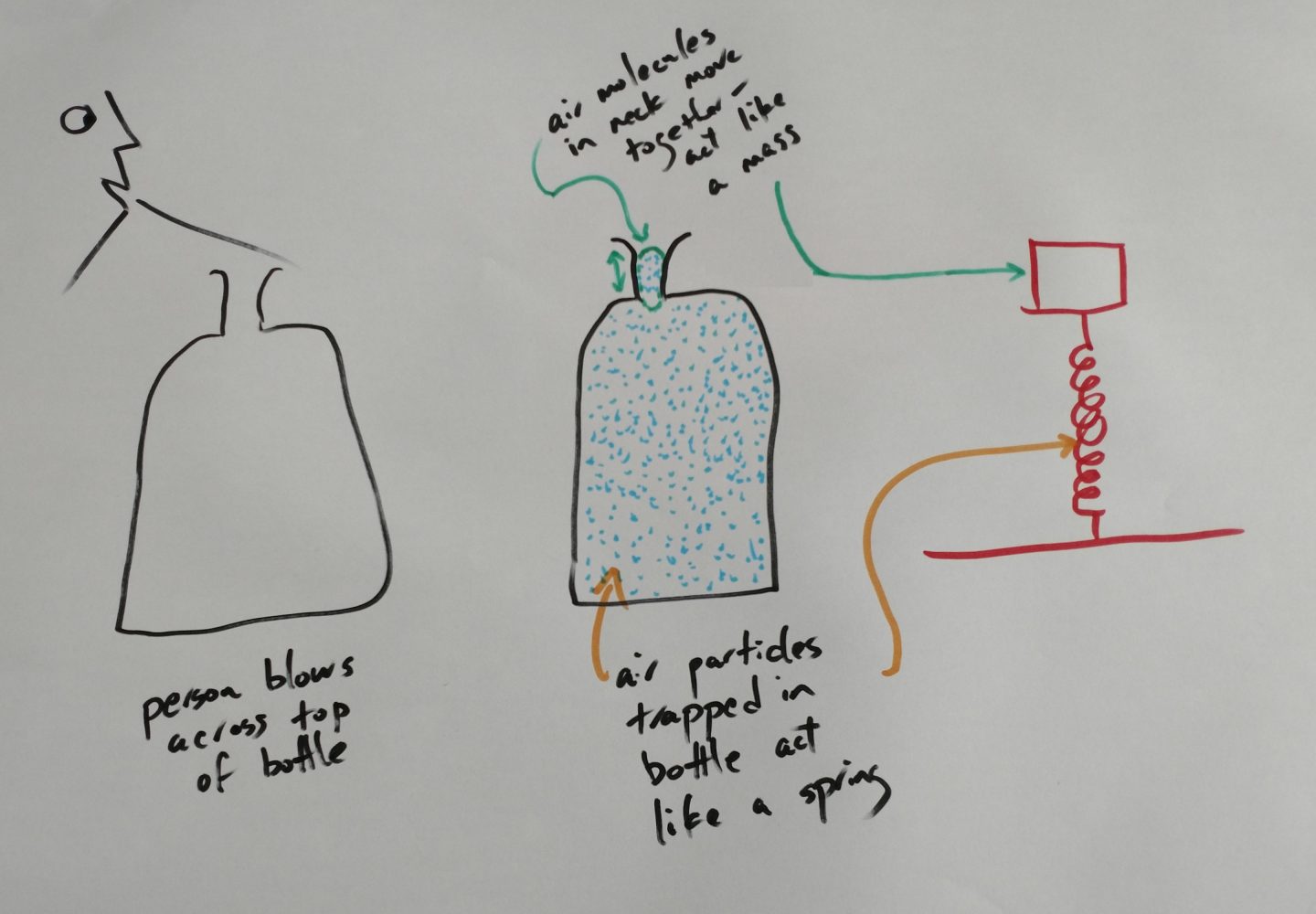
The problem is that most bottles are not column-shaped- the air column model doesn’t account for the difference between the neck and body of the bottle. A new model is needed to deal with the shape of the bottle. Helmholtz appealed to a familiar model to try to explain why wine bottles resonate at the frequencies they do.
Helmholtz imagined the air inside the bottle as a kind of spring-mass system. Helmholtz’ idea was this: think of the plug of air in the neck of the bottle as a mass that bobs in and out of the bottle. The air inside the bottle acts like a “spring.” When the plug of air in the neck goes into the bottle, the air inside the body of the bottle is compressed and pushes the plug of air in the neck out of the bottle. When plug of air in the neck leaves the bottle, the air inside the body of the bottle is stretched and draws the plug back in.
The animation on the UNSW Acoustics Helmholtz Resonance web page [1] shows the basic idea. When you click play, you can see the pressure inside the bottle oscillate as the plug of air in the neck (shown in a very light gray color) moves in and out of the bottle.
Using what he knew about the properties of air and how spring-mass systems work, Helmholtz derived an equation that correctly predicts the resonant frequency of wine bottles (and other cavities with similar shapes). The resonant frequency of a Helmholtz resonator depends on the speed of sound in air (represented by lower case [latex]v[/latex] ), the volume of the body of the bottle (represented by upper case [latex]V[/latex]), the length of the neck ([latex]L_0[/latex]) and the cross-sectional area of the neck ([latex]A[/latex]):
[latex]f_H=\frac{v}{2 \pi}\sqrt{\frac{A}{L_0V}}[/latex]
The lower caserepresents the speed of sound in air; the upper case [latex]V[/latex] is the volume of the body of the vessel. Generally, large resonators with long necks and shall openings have the lowest resonant frequencies. Helmholtz resonators have a single natural frequency- there are no overtones.
What are Helmholtz resonators good for?
Helmholtz resonators have been used for a wide variety of purposes. Helmholtz resonators are not common in musical instruments. Some whistles are Helmholtz resonators. The air cavities in some string instruments (including the guitar) are Helmholtz resonators. Helmholtz resonators are primarily used to damp/trap noises. The Romans and others used vases with a small amount of cloth fiber to damp out undesirable frequencies. Modern airplanes use acoustic panels with Helmholtz resonators to damp out engine noise. Audiophiles and recording studios use slat resonators to “trap” undesirable frequencies. The theory of Helmholtz resonators is widely used in exhaust systems for internal combustion engines and loudspeaker systems (especially ported speakers and subwoofers).
Image credit
Simple model of Helmholtz resonator. Created by Abbott.
- Wolfe, J. (no date). Helmholtz resonance. Retrieved from http://newt.phys.unsw.edu.au/jw/Helmholtz.html ↵
