25 Natural frequency

Forced vibration

Why is it that some bridges have literally shaken apart in heavy wind? How is it that different strings on a guitar produce different pitch from the same pluck? How is that musical instruments produce predictable pitches from seemingly random actions like the pluck of a string, blowing across a hole or dragging the bow across a string?

Objects can force other objects to vibrate. A mallet strikes a tuning fork. Wind rushes past a building or through the wires of a suspension bridge. Heavy machinery shakes the floor. The bow drags across a violin string. This is called forced vibration. What happens next depends not just on the force, but also on the properties of the system being driven.

Natural frequency

Many vibrating systems have a frequency at which they oscillate easily. A classic example is a person on a swing.  Release yourself from some height and you will automatically swing back and forth at a certain frequency. It does not matter how high you start, or whether you pump your arms- the swing will always go back and forth with the same frequency. The swing-person system has a natural frequency– a preferred frequency of vibration. Some systems, like strings and air columns, have more than one natural frequency.  That’s why musical instruments produce overtones.

The natural frequency is set by the properties of the system. The natural frequency of a pendulum is determined by its length (and the strength of gravity). The natural frequency of a spring-mass system is determined by the spring’s stiffness and amount of mass hanging from the spring. The natural frequency of a string is determined by its length, its mass and how tightly the string is stretched.

The easiest way to determine the natural frequency of a system is to give the system a quick shock and watch (or listen) to its response. Give a person on a swing a push and measure the frequency of the resulting motion. Strike a tuning fork (or pluck a guitar string) and find the frequency of the result sound. If the system has a single natural frequency, it will respond by vibrating at that natural frequency. If the system has several natural frequencies, it will respond by vibrating in a complex motion that includes many natural frequencies- almost musical instruments produce overtones because almost all vibrating systems have multiple (but distinct) natural frequencies. Not every system or object has a natural frequency. Give the wall a whack, and it responds with a dull thud. Rub two pieces of sandpaper together and you get noise (i.e. a random mix of wide band of frequencies with no distinct fundamental frequency).

The presence of natural frequencies in a structure can be a blessing or a curse. The presence of natural frequencies in strings allows violinists to reliably produce the pitches they want (and not others). The natural frequencies of the hairs in our inner ear allow us to perceive pitch. The presence of natural frequencies in some objects can can also be disastrous. When exposed to vibrations, such objects can vibrate uncontrollably at their natural frequency- literally shaking themselves to destruction. Examples include  breaking a wine glass with sound ^[1](3:08 youTube video) and  this stunning helicopter accident ^[2](0:37 youTube).

Frequency response

If you sing different notes near a tuning fork, you will notice something remarkable. Most of the pitches you sing will have almost no effect on the tuning fork. However, if you sing at just the right frequency- the natural frequency of the tuning fork- the fork will continue to ring after you’ve stopped singing. Obviously, how the fork responds to your voice depends on the frequency you sing. Replace the tuning fork with something else (like a guitar or the wall) and the results will be different. How a system responds to inputs of different frequencies is called frequency response. Mathematically, frequency response measures how much a system (like the tuning fork or the guitar string) multiplies the amplitude of a given input (like your voice) at different frequencies.

Frequency response is often shown graphically using a frequency response curve.  A frequency response curve looks a lot like an FFT. Frequency is plotted along the x-axis and gain is plotted along the y-axis. (Gain measures how much the system increases the amplitude of the input vibration). The figure below shows the frequency response of a system with just one natural frequency. Notice the tall peak at the natural frequency. Systems with sharp peaks in the frequency response curve are desirable when you want the system to produce only certain frequencies, no matter what the input is.  A tuning fork is an example of a system with a just a few sharp peaks on its frequency response curve.

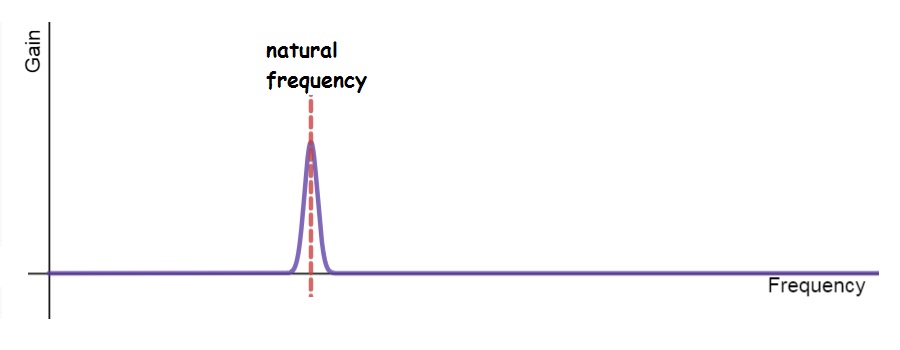
If a system doesn’t have a natural frequency, the frequency response graph has no peaks- the result is often called flat frequency response. Systems with flat frequency response amplify all frequencies equally. Flat frequency response is desirable when you want faithful reproduction of an input signal. For instance, headphones, loudspeakers, microphones and other audio equipment generally strive for flat frequency response. A wall can amplify sounds- try pressing a music box or a tuning fork against a wall- but the frequency response is pretty flat. Try different tuning forks, and you find that the wall amplifies different frequencies equally well.  Press a music box pressed against the wall and you’ll notice that no single note sticks out- all the pitches are amplified by about the same amount.

In principle, you can also determine the frequency response of a system by exposing it to noise. If the system has a natural frequency, the natural frequency component of the noise will be amplified much more than other frequencies, creating an output with a specific frequency. This is why you hear (faint) pitched sound if you put a tube near your ear in a quiet room.

Resonance

When you use a vibration at a system’s natural frequency to force a system to vibrate, the result is called resonance. The word “resonate” comes from Greek: re- (meaning “again”) and sono- (meaning “sound”). Breaking a wine glass with the human voice relies on resonance. The singer taps the glass to determine its natural frequency. The singer then sings the pitch he/she heard and the glass responds.

Timing is the key to resonance. A kid on a swing set is a system with a natural frequency. If you push the kid on the swing in sync with the motion of natural motion of the swing, each push adds to the kid’s speed, resulting a a thrilling ride. If your pushes are out of sync with the natural swinging motion, not much happens- sometimes your push speeds the kid up and other times the push slows the kid down. Resonance happens when some external driver (like the parent on the swing set) vibrates in sync with the natural frequency of a system (like the kid on the swing).

Resonance can be shown using pendulums of different lengths tied to the same string, as done beautifully by Helen Czerny in this short video from the BBC (2:13 on youTube)^[3]. Pendulums with different lengths have different natural frequencies. When one of the pendulums is set in motion, all the others are forced to vibrate at that same frequency. However, none of the pendulums vibrates very much unless one of them happens to be exactly the same length as the first pendulum.

Hearing and resonance

The deepest part of our inner ear uses resonance to tell our brains which frequencies are in the sound that enters the ear. Inside our ears are thousands of hair cells, each with a different natural frequency. When sound gets to the inner ear, some hairs (those with natural frequencies that match the frequencies present in the incoming sound) vibrate, while others don’t. These hairs are connected to nerve cells which fire, letting our brains know which hairs are being vibrated and how.

Resonance of the air column in our ear canal also plays a minor role in our hearing. Because of the ear canal’s length (typically about 2.5 cm), our ear canal amplifies sounds in the 2000 Hz to 3000 Hz range. This is especially useful for hearing human speech.

“What’s up with noises?” (12:48 on youTube) is a fast-paced, entertaining overview of vibrations, resonance, hearing and swings.  ^[4]

Not resonance

Do not confuse resonance with amplification. Not all amplification is caused by resonance. For instance, you may have noticed that the ringtone of your cell phone is amplified when the phone sits on a table. This amplification is not an example of resonance.

Resonance refers to a very specific situation- amplification that is caused when one thing vibrates at the natural frequency of another. In order to resonance to occur, two things must both be true:

1. First, the system that is being vibrated must have a natural frequency and, 
2. Second, the source that is forcing that system to vibrate must be vibrating at the natural frequency of the system that’s being vibrated. 

The reason that the cell phone example isn’t resonance is that the table doesn’t have a natural frequency. The table has a relatively flat frequency response that amplifies a wide range of frequencies well- not just one. It doesn’t matter which ringtone you choose, the table will amplify it.

Some textbooks give the Tacoma Narrows bridge disaster as an example of resonance, but, strictly speaking, Tacoma Narrows isn’t resonance, either. Even though the bridge clearly has a natural frequency, the stimulus that caused the disaster is the wind, which is not a vibration at all. By this strict definition, a plucked guitar string is not an example of resonance either- again, the stimulus (the pluck) is not a vibration. However, if you sing at one of the string’s natural frequencies, the string’s response is considered resonance because the string is responding at its natural frequency and the stimulus (your voice) is a vibration at the natural frequency of the string.