36 Beats

What are beats?

If you’re a musician, you’ve probably heard the sound that results when you two sounds with almost the same pitch are played together. The result is sound with a distinctive “wah-wah-wah” sound. The pitch is about the same as the two sounds that are combining, but there is a characteristic “in and out” sound as the sound cycles back and forth between being loud and being soft. This sound is called beats. If the two notes creating the beats are really close together, the “beating” is slow- the “wahs” are long and the silences in between don’t occur very often- the beat frequency is low. If the two notes are farther apart, the beat frequency is higher- the “wahs” happen more often.  Musicians use beats to tune musical instruments. (This video shows how to tune a bass guitar using beats)^[1].

If you’ve never heard beats before, here are some online resources to check out:

• An interactive beats generator, ^[2] and/or
• Lots of info and recordings of beats. ^[3] Scroll to the bottom of the page to see the recordings.
• Physics classroom demo using tuning forks. ^[4]

What’s happening?

What causes beats?

Beats are another example of interference. As the two sounds that are being played together drift into and out of phase, the two waves shift back and forth from constructive interference to destructive interference. The silence between the “wahs” is caused by destructive interference between the two source sounds.

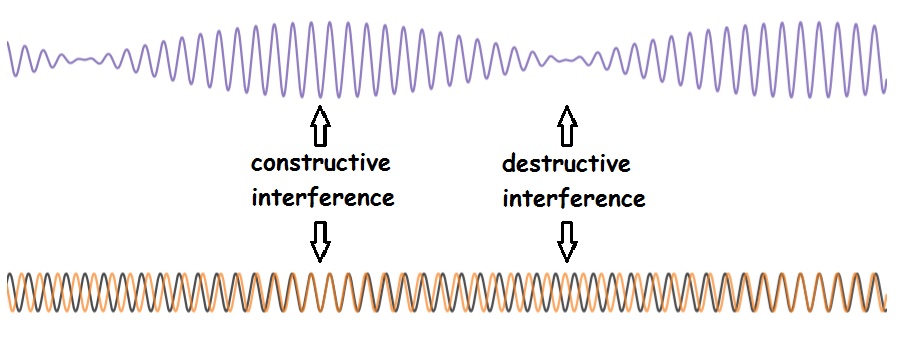
If the two source frequencies are nearly identical, it takes a very long time for the sounds to drift into (or out of) phase. This results in a low beat frequency. If the frequencies are farther apart, the two sounds drift in and out of phase more often, resulting in a higher beat frequency. The math is simple:

[latex]f_b = |f_1-f_2|[/latex]

In this equation, [latex]f_b[/latex] represents the beat frequency; [latex]f_1[/latex] and [latex]f_1[/latex] represent the frequency of the sounds causing the beats. If a 100 Hz sound is played with a 98 Hz sound, the result is a sound with a beat frequency of 2 Hz (according to the equation). In practical terms, there will be two full “wahs” per second. If the two sounds start in phase, they won’t be in phase again until the two source sounds drift out of phase by exactly one full cycle. Each second, the 100 Hz gains two full cycles on the 98 Hz sound, so the sounds are in phase twice every second.

At the beginning of this section on beats, it was mentioned that the listener hears a single note that fluctuates in volume (at the beat frequency). It seems logical that the frequency of this single note would be halfway between the two frequencies being played together. With a little math beyond the scope of this book you can show that your intuition is correct:

[latex]f = \frac{f_1+f_2}{2}[/latex]

So, if you play a 98 Hz note and 100 Hz note together, you hear a 99 Hz note that goes through two full cycles of “loud-soft” each second.

Human perception and beats

When the difference between the two sound frequencies is small (less than 10 Hz for most people), people hear a single pitch that varies in loudness. As the beat frequency increases, two things happen. First, our ears/brains have trouble keeping up with the rapidly changing amplitude and we lose the ability to hear the individual silences between the “wahs.” Second, our brains begin to recognize the difference between the two pitches creating the beats. For most people, this transition happens when the difference between the two frequencies is in the 10 Hz to 50 Hz range. If the difference between the two sound frequencies becomes large enough, difference tones (sometimes called Tartini tones, after the violinist who discovered them) occur. Listeners hear not only the two source frequencies, but also a third (much lower) tone. This tone usually corresponds to a frequency equal to the difference of the two source frequencies. One example of this is a London police whistle. The whistle has two chambers, each of which plays a different very high note. When the whistle is sounded, listeners hear three notes together- the two high notes and a third note much lower than the other two. For musicians, beats enter into the perception of intonation. To hear some of these effects, check out the movies and recordings on the PhysClips page on beats and difference tones.

Image credit

Beats: Two sine waves (lower panel) interfere to produce beats (upper panel). Created by Abbott using desmos.com