26 Vibrating strings

Stringed instruments

String instruments are common to many cultures. These pitched musical instruments rely on one of the simplest common resonating systems around- stretched string. Understanding a simple model of a string goes a long way to explaining how string instruments work and how to play them.

Model of a string

Stretch a slinky between two people and have one of the people shake their end. You will rapidly discover that only certain frequencies will be easy to keep going. At each one of these frequencies, the string produces a distinct pattern. These patterns are called standing waves. Standing waves can only occur at certain frequencies. The waves produced by the hand interfere with the reflections from the opposite end of the string. If the timing is just right, the reflected pulses constructively interfere with the new waves produced by the hand (and interfere destructively at the nodes). The correct timing produces nodes at both ends of the string. If the timing is off, no coherent pattern is produced.

Standing waves have the same characteristic shape as the familiar traveling waves, but instead of moving left or right, the wave shape bobs up and down. Real strings vibrate too fast for the eye to see. When you look at a vibrating string, you’ll see an “envelope” of the motion as the string moves back and forth between two extremes. The diagram below shows three different standing wave patterns as they are usually displayed in books. The string wiggles back and forth between the location of the solid line and dotted line.

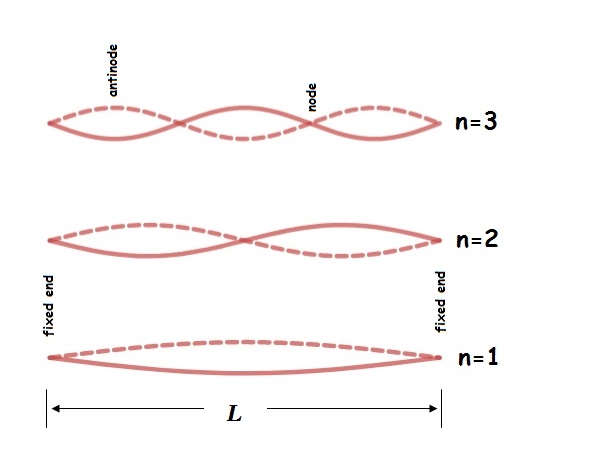
Each pattern is called a mode and each mode is labeled with a number that corresponds to the number of loops (“footballs”) in the pattern. The pattern labeled n=1 is the fundamental- it has the longest possible wavelength (and lowest frequency) of any standing wave that can be formed on the string. Other modes have more loops, shorter wavelengths and higher frequencies. There are some points on the string that never move (called nodes). There are always at least two nodes on a string- one at each end where the string is held fixed. The places where the movement is the largest are called antinodes.

Diagrams are helpful, but it’s important to look at video, too. Check out the Wikimedia Commons animated gif ^[1] and/or the animations on Dan Russell’s standing wave webpage . ^[2] These (slowed down) animations  show the motion of the string. The animations clearly show that different modes vibrate different frequencies. Modes with more “footballs” vibrate at higher frequency. If you look close at the animations, you’ll notice that the n=2 pattern completes 2 full cycles in the time it takes the n=1 to complete one cycle (and the frequency of the n=3 mode is three times the frequency of the n=1 mode and so on).

Wavelength of a standing wave

The distance from one node to the next node equals half the wavelength of the standing wave. Put another way, wavelength of a standing wave equals the length of two “footballs.” If you look at the n=2 or n=3 pattern, you will notice that a full cycle (up and down) of the dotted line extends over two “footballs”- not just one. To understand why, look at the diagram above for n=2 or n=3. Notice that going from one node to the next covers only half a cull cycle of the wave.

Wavelengths of different modes

Standing waves on strings only happen when a whole number of “footfalls” fit between the two fixed ends of the string. The distance between the two fixed ends of the string is called the string length, and is usually represented by [latex]L[/latex].  The wavelength on a standing wave on string only depends on the string length and the number of “footballs.” The equation is

[latex]\lambda_n = \dfrac{2L}{n}[/latex]

where [latex]L[/latex] represents the length of the string and n represents the mode number (or the number of foot balls). To find the wavelength of any given mode, divide the wavelength of the fundamental mode by the mode number.

Here’s the logic behind the equation. For a standing wave with a certain number of loops, the length of each “football” is simply the string length divided by the number of “footballs.” The wavelength is double that- remember that it takes two “footballs” to make one complete cycle of a standing wave. Notice that wavelength of the fundamental mode is twice the string length.

Frequencies of different modes

Different frequencies produce different standing wave patterns. The lowest frequency that produces a standing wave produces a “one football” shape. As you increase the frequency, standing waves with more and more “footballs” appear and disappear. Every time the frequency is just right, a pattern with a whole number (1, 2, 3, 4, 5, etc.) of footballs emerges.

The frequencies of the different modes follow a simple pattern. The frequency of the n=2 mode is twice the fundamental frequency; the frequency of the n=3 mode is three times the fundamental and so on. Put in equation form,

[latex]f_n = n f_1[/latex]

The equation summarizes the simple rule of thumb above- the frequency of an given mode equals the frequency of the fundamental times the number of “footballs” in its standing wave pattern.

Where does the equation [latex]f_n = n f_1[/latex] come from? The equation follows directly from the equation for wavelength above ([latex]\lambda_n = 2L/n[/latex]) and [latex]v = f\lambda[/latex]. Here’s the logic. The speed of waves is the same for all the standing waves on a particular string, you can write [latex]v = f_n\lambda_n[/latex]. Notice that the wave speed has no subscript- the speed of waves is the same for every single mode. To show that [latex]f_n = n f_1[/latex], start with [latex]v=\lambda_n f_n[/latex], then replace  [latex]\lambda_n[/latex] with [latex]2L/n[/latex] and solve the resulting equation for [latex]f_n[/latex]. The result is

[latex]f_n = n \dfrac{v}{2L}[/latex]

This new equation essentially proves that [latex]f_n = n f_1[/latex], because [latex]f _1 = (v/2L)[/latex].

In all of the equations above, it is important to keep in mind that standing waves in a string exist on the string- not in air. This means that [latex]v[/latex] in all these equations refers to the speed of waves in a particular string- not the speed of sound in air!

This video (made by two PHY103 students at Buffalo State College in Spring 2018) is an excellent summary of standing waves on a string ^[3] .

Speed of waves on a string

The speed of waves in any medium only depend on the properties of the medium. It’s no different for strings. The relevant equation is

[latex]v = \sqrt{\dfrac{T}{\mu}}[/latex]

In this equation, the capital Roman letter T represents tension and Greek letter [latex]\mu[/latex] (mu) represents the string density. Tension is a measure of how tightly the string is stretched. String density is a measure of how much mass a string has per unit length.

What does this equation mean? First, tension and wave speed are directly related- on any given string, waves travel faster when string tension is greater. This is part of the reason that the pitch of a string goes up when you tighten up the string. The density of the string matters, too, but wave speed and string density are inversely related- for strings that have the same tension, heavier strings have lower waves speeds. This partly explains why the thickest, heaviest strings typically produce the lowest notes on a string instrument.

Image credits

Standing wave patterns on a string of length L fixed at both ends. Created by Abbott using desmos.com.