Traveling waves
22 Doppler effect
That distinctive sound…
If you’ve ever watched a race car, you’ve heard the dramatic drop in pitch that happens the moment a car screams past. If you’ve never heard it, check out this short youTube clip from the Kansas Speedway [1] or this one of an Amtrak train [2] or check out Neil deGrasse Tyson’s impression of NASCAR [3].
Ever wondered what the race car driver hears? If you’ve watched on TV, you know the driver does not experience the drop in pitch that the roadside listener hears. All the driver hears is the constant whine of the engine- check out this cockpit recording from a NASCAR race. [4] Why do the driver and the roadside listener hear different sounds from the exact same source? Why does the sound the race fan hears change, even though the sound put out by the engine doesn’t? The short answer is movement.
What Doppler effect is (and why it happens)
Doppler effect refers to the difference between the frequency a detector measures and the frequency a wave source actually produces. The difference is due to the relative movement of source and detector. The phenomenon was first noticed with light waves, but applies to all kinds of waves (including sound waves).
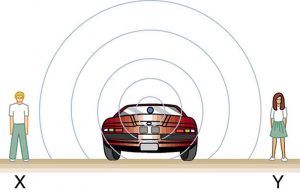
How can the frequency you hear be different than the frequency a sound source produces?
Doppler effect can happen if the detector is moving (even if the source isn’t). Imagine yourself sitting at the end of the conveyor belt coming from a candy factory. If neither the detector (you) nor the source (the factory) is moving, the detected frequency matches the source frequency. Put another way, if you sit at the end of the conveyor belt and the factory makes five candies a minute, you get five candies a minute.
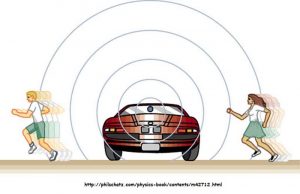
But if you are walking toward the candy factory along the conveyor belt, the situation changes- you now encounter more than five candies a minute (because you are moving toward the source)- even though the factory is still producing five candies a minute. Now, detected frequency (how often you get candies) is higher than source frequency (how often the factory makes candies). If you move away from the source, a similar thing happens. This time the detected frequency is lower than the source frequency.
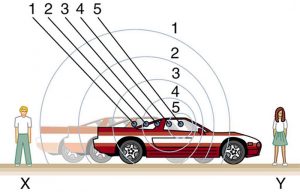
Doppler effect also happens when the source is moving and the detector is stationary. If a wave source is stationary, the source makes ripples that are concentric circles and waves arrive at your location at the same frequency that the source makes them. However, if the source is moving toward you, each new wave is made closer and closer to your location. Because each ripple is made closer to you than the last, you receive ripples at a higher frequency than the source makes them. If you the source is moving away from you, the each ripple is made farther and farther from your location, resulting in a lower (detected) frequency. With the moving source, the wave pattern is also affected- ripples bunch up in front of the moving source and spread out behind it.
Stop to think
- What is Doppler effect? When does it occur?
- Is the Doppler effect real or an auditory illusion?
If the wave source is moving faster than the waves it creates, something interesting happens- there are no waves in front of the source. Behind the source, each ripple the source makes overlaps with previously made ripples, creating a cone that moves along with the source. In the case of water waves, this “cone” is a two-dimensional V-shape.

For sound, this shock cone is the cause of “sonic boom”- listeners hear a loud “boom” when the cone (caused by an airplane moving faster than the speed of sound) passes their ears.

Doppler effect happens whenever the distance between source and detector is changing, but the math gets trickier. Whenever the source is getting closer to the detector, the detected frequency is higher than the source’s frequency. Whenever the source is getting farther from the detector, the detected frequency is lower than the source’s frequency. This is why the race fan hears a high pitch (while the car is approaching) followed by a lower one (as the car goes away). If the source to detector distance isn’t changing, the detected frequency will be the same as the source’s frequency. The race car driver always hears the same frequency sound that the engine produces- the distance between source and detector isn’t changing even though both car and driver are moving quickly.
How big is the Doppler effect? The answer depends on how quickly the distance between source and observer is changing- the faster the source to detector distance is changing, the bigger the effect. With sound waves, the speed of sound also plays an important role in Doppler effect. In order for Doppler effect to be noticeable, either the source or the detector must be moving pretty fast. That’s why we notice Doppler effect at a car race and not when we’re talking while passing each other in the hall. If either the source or the detector are moving at (or near) the speed of sound, crazy things (like sonic booms) can happen.
The math
The full Doppler effect equation is
[latex]f_{obs} = f_{source} \left(\dfrac{c+v_{obs}}{c - v_{source}}\right)[/latex]
Here’s what the symbols mean:
| Symbol | Meaning | Use a positive number… |
| [latex]f_{obs}[/latex] | frequency at the observer | always |
| [latex]f_{source}[/latex] | frequency of the source | always |
| [latex]c[/latex] | speed of the wave | always |
| [latex]v_{obs}[/latex] | speed of the observer | if observer is moving toward the detector |
| [latex]v_{source}[/latex] | speed of the source | if source is moving toward the observer |
Be careful about the algebraic signs for [latex]v_{obs}[/latex] and [latex]v_{source}[/latex]!
- Use a positive number for [latex]v_{obs}[/latex] if the observer is moving toward the source
- Use a positive number for [latex]v_{source}[/latex] if the source is moving toward the observer
- Use a negative number for [latex]v_{obs}[/latex] if the observer is moving away from the source
- Use a negative number for [latex]v_{source}[/latex] if the source is moving away from the observer
Always check your answer. If the distance between source and detector is shrinking, [latex]f_{obs}[/latex] should be greater than [latex]f_{source}[/latex]. If the source and detector are getting farther apart, [latex]f_{obs}[/latex] should be less than [latex]f_{source}[/latex].
When the source is stationary, [latex]v_{source}=0[/latex] and the equation simplifies to
[latex]f_{obs} = f_{source} \left(\dfrac{c + v_{obs}}{c}\right)[/latex]
When the detector is stationary, the equation simplifies to
[latex]f_{obs} = f_{source} \left(\dfrac{c }{c- v_{source}}\right)[/latex]
For more detail on the math, check out Michael Fowler’s Doppler Effect webpage.
Example problem: An car race car going 100 m/s emits a sound that has a frequency of 700 Hz. What frequency will a fan in the stands hear as the car is approaching? What frequency will the fan hear just after the car passes? What frequency does the driver hear?
Example: A day at the races
QUESTION:
A typical Indy car runs at a speed of about 100 m/s, emitting a whine at about 700 Hz. What frequency will a fan in the stands hear as this car approaches? What frequency will the fan hear just after the car passes? What frequency does the driver hear?
SOLUTION:
Identify important physics concept: This problem is about Doppler effect. The sound the observer hears depends on how the source and observer are moving. If the sound source is moving towards the listener, the listener will hear a higher pitch than the engine is making. The important equation is
[latex]f_{obs} = f_{source} \left(\dfrac{c+v_{obs}}{c - v_{source}}\right)[/latex]
Diagram: You might make three diagrams for this problem- one for each part. What’s important here is how source and detector are moving in each case.
List known and unknown quantities (with letter names and units):
For all three parts of this problem, we’re asked to find the frequency heard by an observer: [latex]f_{obs}[/latex]. For each part, we know the frequency of the source ([latex]f_{source}=700 \: Hz[/latex] for all the different scenarios) and speed of both the observer and source. We need to look up the speed of sound. We will use [latex]c=343 \: m/s[/latex]. Here’s a summary:
| What race fan hears as car approaches | What the race fan hears after car passes | What driver hears |
| [latex]f_{obs}= \: ?[/latex]
[latex]f_{source}=700 \: Hz[/latex] [latex]v_{obs}=0 \: m/s[/latex] [latex]v_{source}=100 \: m/s[/latex] |
[latex]f_{obs}= \: ?[/latex]
[latex]f_{source}=700 \: Hz[/latex] [latex]v_{obs}=0 \: m/s[/latex] [latex]v_{source}=-100 \: m/s[/latex] |
[latex]f_{obs}= \: ?[/latex]
[latex]f_{source}=700 \: Hz[/latex] [latex]v_{obs}=+100 \: m/s[/latex] [latex]v_{source}=-100 \: m/s[/latex] |
For part c (what the driver hears), I assumed the engine was in front of the driver. If you assume the engine is in the back, you will have [latex]v_{obs}=-100 \: m/s[/latex] and [latex]v_{source}=+100 \: m/s[/latex]. At the end of the problem it won’t matter- the answer will be 700 Hz either way. (Keep in mind that the driver and engine are not getting closer together or farther apart, so the driver hears the same sound the engine puts out.
Do the algebra: The equation is already solved for [latex]f_{obs}[/latex], so there’s no algebra to do.
Do unit conversions (if needed) then plug in numbers: Units are are all consistent here- no need for unit conversions, so we’re ready to plug in the numbers:
What the race fan hears as car approaches:
[latex]f_{obs} = f_{source} \left(\dfrac{c+v_{obs}}{c - v_{source}}\right)=(700 \:Hz) \left(\dfrac{343 \:m/s+0}{343 \:m/s - 100\:m/s}\right)[/latex]
[latex]f_{obs} =(700 \:Hz) \left(\dfrac{343 \:m/s}{243 \:m/s }\right)=988 \:Hz[/latex]
What the fan hears just after car passes:
[latex]f_{obs} = f_{source} \left(\dfrac{c+v_{obs}}{c - v_{source}}\right)=(700 \:Hz) \left(\dfrac{343 \:m/s+0}{343 \:m/s - (-100\:m/s)}\right)[/latex]
[latex]f_{obs} =(700 \:Hz) \left(\dfrac{343 \:m/s}{443 \:m/s }\right)=542 \:Hz[/latex]
What the driver hears:
[latex]f_{obs} = f_{source} \left(\dfrac{c+v_{obs}}{c - v_{source}}\right)=(700 \:Hz) \left(\dfrac{343 \:m/s+100 \:m/s}{343 \:m/s - (-100\:m/s)}\right)[/latex]
[latex]f_{obs} =(700 \:Hz) \left(\dfrac{443 \:m/s}{443 \:m/s }\right)=700 \:Hz[/latex]
Reflect on the answer:
- Answer matches the video evidence: The race fan hears a pitch that starts high, then drops dramatically at the moment the car passes; driver hears unaltered engine noise the entire time!
- Pitch change the roadside listener hears is dramatic (because the speed is so high)! The frequency is cut almost in half. That’s nearly a one octave drop in pitch!
Simulations and other resources
- The wikipedia article on Doppler effect [5]is thorough and includes some useful animations and a recording. Animations show moving source at various speeds, including faster than the wave (sonic boom/bow wave).
- The UNSW Physics Doppler effect web page [6]has recordings, videos and animations.
- This webpage designed for a class on Doppler effect [7]shows five helpful animations. In class, students measured the frequencies of source and observer for each of the five scenarios shown. (There is a “clock” in the simulation).
Stop to think answers
- Doppler effect describes the difference between the frequency the wave source puts out and the frequency of waves arriving at the receiver. Doppler effect occurs whenever the distance between a wave source and a wave receiver is changing.
- Doppler effect is very real. The frequency the receiver gets is physically different than the frequency the source produces.
Image credits
- Cartoons of cars and people: https://philschatz.com/physics-book/contents/m42712.html
- Bow and tail waves from a boat: https://commons.wikimedia.org/wiki/File:AmsterdamRijnKanaal_880.jpg
- Ripple patterns caused by a plane a three different speeds: https://commons.wikimedia.org/wiki/File:Sonic_boom_diagram.png
References
- Koch, W. (2016, February 11). Doppler effect at Kansas Speedway. Retrieved from https://youtu.be/_UPQeKEXr8Q ↵
- SpeakerPolice. (2010, March 30). Amtrak with great Doppler effect. Retrieved from https://youtu.be/ly0Luc2AdoU ↵
- Mashable Deals. (2017, August 10). NASCAR doesn’t like the Doppler effect. Retrieved from https://youtu.be/B0yy97brmB0 ↵
- Gomez, J. (2016, February 21). 2016 Nascar Daytona 500 | Last Laps - EPIC! Retrieved from https://youtu.be/iPSj0Qjh00I ↵
- no author (2019, December 17). Doppler effect. Retrieved from https://en.wikipedia.org/wiki/Doppler_effect ↵
- UNSW Physics (no date, accessed January 17, 2020). Doppler effect. Retrieved from https://www.animations.physics.unsw.edu.au/jw/doppler.htm ↵
- Christian, W. (2014). Doppler effect simulation. Retrieved from https://www.compadre.org/osp/EJSS/3858/38.htm on January 17, 2020 ↵
