Useful Info
46 Solving physics problems
Stay organized!
Over the last twenty years, I’ve watched lots of students struggle doing physics problems on homework sets and tests. I’ve seen them get wrong answers and not be able to track down their mistakes. Sometimes, it’s because the student is confused about the physics. More often, though, it’s because the student is trying to “jump to the answer”- trying random things in hopes of pumping out a right answer quickly. It works (sometimes), too- otherwise students wouldn’t do it. But it is a recipe for disaster for anything but the simplest “formula plug and chug” type of textbook exercises.
The key to solving science problems reliably and quickly is a systematic approach. Worked examples in physics books follow a common format- with good reason. The exact method varies, but the basic steps are universal. Versions of the template below have been published in education journals and are written into almost every physics textbook. Physicists use this approach because it works. Learn the method and use it!
At first, you might think this method is a waste of paper and/or time. Over time, you will develop your own streamlined version of this template- and that’s great. However, keep the essential elements in mind- 1) stay organized and 2) write all the important stuff down- and you can expect success.
Physics problem solving template
- Identify the important physics concept in the problem. In this book, one sentence and one equation are usually enough.
- Draw an appropriate diagram. In many problems, a diagram will help you remember and/or recognize important details.
- List known and unknown quantities with letter names and units. This step is crucial. It is where you get organized. It is where you identify the info that will help you get to the answer (as well as irrelevant info put there to distract you). Get these details right, or expect trouble down the road.
- Do the algebra. This means turning the equation(s) around so that the quantity you want to find is alone on the left hand side of the equation. Don’t plug in any numbers yet!
- Do any necessary unit conversions and then plug in numbers. Do unit conversions (if needed). Replace the letters in equations with the correct numbers. Then pull out the calculator.
- Reflect on the answer. There are two basic things to think about here:
- Could the answer possibly be correct? Does it have the right units? Is it in the right “ballpark”?
- What did you learn from the problem? Pay attention to what just happened. Did you have any questions? Was there anything that made you stop and take notice?
Don’t believe me?
Check out these websites. Their advice has a lot in common with mine…
- http://blog.cambridgecoaching.com/4-tricks-for-solving-any-physics-problem
- http://www.smarterthanthat.com/physics/physics-dont-panic-10-steps-to-solving-most-physics-problems/
- https://youtu.be/YocWuzi4JhY
- https://youtu.be/ywZPAsM1FeU
An example
Keep in mind that the example you are about to read is written by a textbook author for a physics student. When you write your own solutions, you will be writing for your own study purposes, or perhaps for a grader. What you produce will almost certainly involve a lot of shorthand- and that’s OK.
Example: To the bat cave
QUESTION:
Bats figure out the distance to nearby objects by emitting short bursts of ultrasonic sound and “listening” for the echo. Fred, the house bat, emits a 50 kHz ultrasonic “chirp” that lasts for just 0.1 milliseconds and hears the echo 8.0 ms later. How far away is the obstacle that caused the echo?
SOLUTION:
Identify important physics concept: This problem is about how sound travels. The important physics to know is that sounds in air all travel at the same constant speed- no matter what. The important equation is
[latex]v = \frac{d} {t}[/latex]
Diagram: A diagram for this problem underscores an important feature in this problem: sound goes from the bat to the obstacle and back again before the bat hears the chirp.
List known and unknown quantities (with letter names and units):
This problem provides too much information . Knowing the physics helps sort the useful info from the useless. To solve the problem, all that’s really needed is 1) the speed of sound in air and 2) the amount of time it takes for the sound to travel from bat to obstacle. The “50 kHz” is irrelevant- all sound travels at the same speed, no matter what the frequency is. How long the sound lasts- the “0.1 milliseconds”- is also irrelevant. I do, however, need to know the speed of sound in air- Google says it’s 343 m/s at 20 °C (room temperature). Since the problem did not provide the temperature, I will assume the air in the cave is at 20 °C.
[latex]d = ?[/latex]
[latex]v=343 \: \frac{m}{s}[/latex]
The sound takes 8.0 ms for the round trip from bat to obstacle and back, so it takes sound half that time to go one way. (The problem asks for the distance from bat to obstacle- not distance from bat to obstacle and back).
[latex]t=4.0 \: ms[/latex]
Do the algebra: Solve [latex]v = \frac{d} {t}[/latex] for distance: [latex]d=vt[/latex]).
Do unit conversions (if needed) then plug in numbers: Units are not consistent here- speed is given in m/s and time is milliseconds- so unit conversion is needed. It’s probably easiest to convert the milliseconds to seconds:
[latex]4.0 \: ms =0.004 \: s[/latex]
Then plug the number into the equation:
[latex]d=vt=(343 \: m/s)(0.0040 \: s)=1.36 \: m[/latex]
Reflect on the answer:
- Answer is pretty small- 1.36 meters is a little more than a yard?! This bat’s really close to something! Is that right? Yes, as it turns out. Google the speed of sound in feet per second, you get 1125 ft/sec- or about 1.1 ft per millisecond. (Sound engineers routinely approximate the speed of sound as 1 foot per millisecond for figuring time delays on stage).
- Units work.
How it looks on a student paper
Obviously, as a student, you aren’t going to write out all the steps the same way a textbook author does- it’s just too time consuming. The picture below shows what a student solution for the bat-obstacle problem above might look in a student notebook or homework paper. Notice that the essential elements are all here- a sketch, a list of known and unknown quantities with units, algebra, numbers plugged in with units and a short evaluation of the answer.
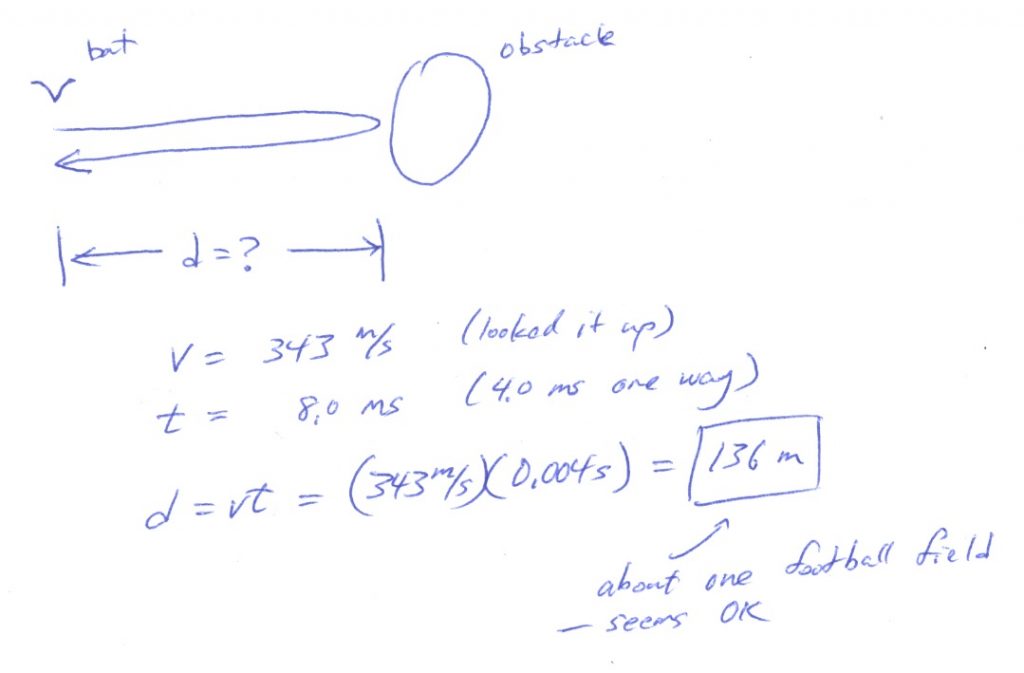
Students who are a little more careful might also include additional stuff, like a list of the extraneous givens (the 50 kHz and 0.1 ms) and why each could be ignored and/or a note about the pitfalls in the problem (“don’t forget to divide by two for out and back”).
