Vibrations
6 More about overtones
What do the vibrations of different string instruments have in common? How are vibrations from a string different than those of a tuning fork or a chime? The secret lies in how the overtones are related to the fundamental.
Overtones and musical instruments
The parts of musical instruments- strings, vibrating columns of air, drum heads- vibrate in complex ways, producing overtones. The overtones a musical instrument produces play a role in the way the instrument sounds.
Many vibrating systems- like strings and columns of air- produce overtones that are whole number multiples of the fundamental frequency. Overtones with frequencies that are whole number multiples of the fundamental frequency are called harmonics. The human voice produces harmonics. So do string instruments (like piano, guitar, and violin) and most wind instruments (like flute and trumpet). No matter what the fundamental is, all these instruments produce overtones at whole number multiples of the fundamental. When a cello plays a note with a fundamental frequency of 100 Hz, the note contains overtones at 200 Hz, 300 Hz, 400 Hz, 500 Hz and so on. A 400 Hz note from a flute has overtones at 800 Hz, 1200 Hz, 1600 Hz, etc. Expressed mathematically, the frequencies produced by these instruments are (f, 2f, 3f, 4f…) where the letter f represents the fundamental frequency. Later in the book, you’ll learn why strings and air columns produce harmonics.
Some systems (like vibrating membranes, vibrating bars and bells) produce overtones that are not harmonics. The overtones are multiples of the fundamental, but the multiples are not whole numbers. For example, all chimes (vibrating metal bars) have overtones at 2.76 times the fundamental, 5.40 times the fundamental, 8.93 times the fundamental (and other higher multiples of the fundamental). Overtones that are not harmonics can be called anharmonic overtones, but most authors simply call them overtones.
An aside about language. Harmonics are a special type of overtone, just like squares are a special type of rectangle. Sometimes, people use the word “rectangle” to mean any rectangle that’s not a square- even though a square is a type of rectangle. They use the word “square” when they mean the rectangle with equal sides. Similarly, people sometimes use the word “overtone” to specifically mean “anharmonic overtone,” assuming you would use the word “harmonic” to refer to overtones that are whole number multiples of a fundamental.
The overtone structure of a vibrating system, written as multiples of the fundamental frequency, is called spectral content. Strings, voice and most wind instruments all share the same harmonic content: (f, 2f, 3f, 4f…). All chimes share the same spectral content: (f, 2.76f, 5.40f, 8.93f…). Some winds (like slide whistles and organ pipes that are closed at one end) only produce only produce odd harmonics- a spectral content of (f, 3f, 5f, 7f…). Spectral content is part of the reason that all chimes sound like chimes and all chimes sound different than strings.
Stop to think 1
Which of these vibrations might have been made by a string instrument? a slide whistle? a chime?
- Vibration A has a fundamental of 100 Hz and overtones at 300 Hz, 500 Hz, 700 Hz and so on
- Vibration B has a fundamental of 200 Hz and overtones at 400 Hz, 600 Hz, 800 Hz and so on
- Vibration C has a fundamental of 300 Hz and overtones at 600 Hz, 900 Hz, 1200 Hz and so on
Different notes on the same instrument
When a musical instrument plays different notes, the fundamental frequency and all the overtone frequencies change, but the spectral content doesn’t. The FFT below shows what happens for a sound with harmonics when the fundamental doubles.
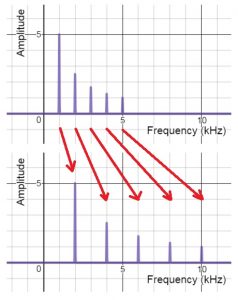
Notice that all the frequencies in the sound- not just the fundamental- double when the fundamental doubles- that’s how the harmonics remain harmonic. If the fundamental changes by certain factor, the overtones all change by that same factor. If the fundamental frequency of a tuba note triples, so do all the overtones in the tuba’s sound. This is true for all types of spectral content- not just harmonics. If the fundamental of a kettle drum goes down by 10%, all the kettle drum’s overtones also drop 10%.
Stop to think 2
One vibrating metal bar on a glockenspiel has a fundamental of 200 Hz and overtones at 520 Hz and 1080 Hz. Does the glockenspiel have the same spectral content as a chime?
Stop to think 3
One vibrating metal bar on a glockenspiel has a fundamental of 200 Hz and overtones at 520 Hz and 1080 Hz. What overtones would the 400 Hz metal bar on the glockenspiel have?
For musicians: Harmonics and musical intervals
If you’re a musician, this section might help put harmonics into perspective. If you’re not a musician, skip this section. The word harmonic derives from the Greek word meaning “agreement.” Western music theory is originally built built on the math of whole number ratios. The figure below shows how harmonics relate to (Western) musical intervals.
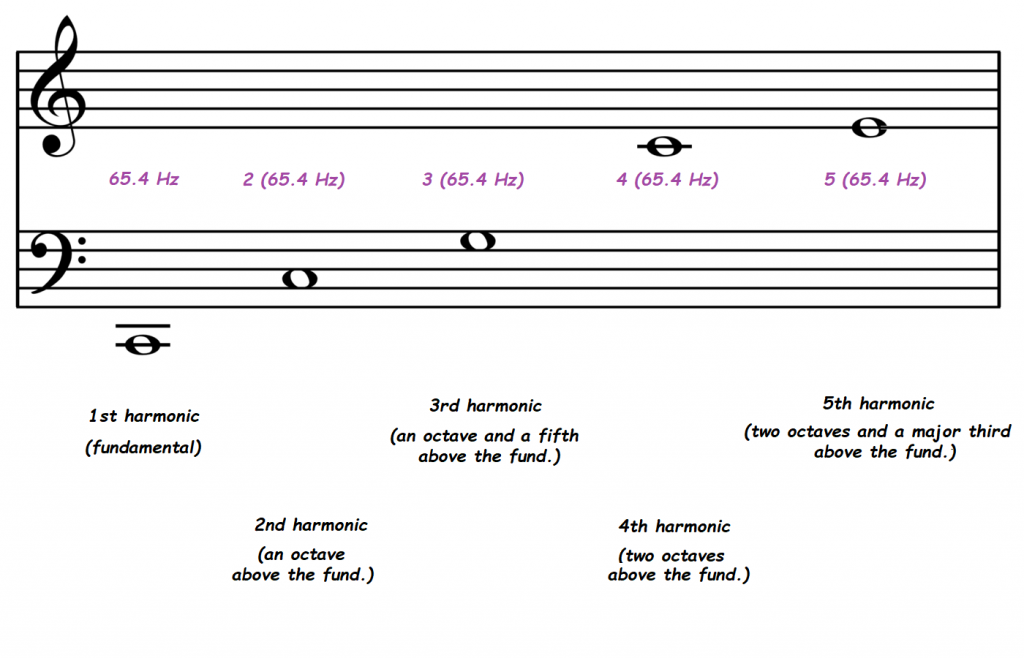
If you’re a string player or a brass player, this series of notes is familiar. For strings players, the overtones are ghostly sounding notes you make when you touch the string lightly at various points. Touching the string at the middle gives the second harmonic. Touching lightly at one-third the string length (e.g. 7th fret on guitar), gives the third harmonic and so on. For brass players, this is almost the same series of notes you get all with the same fingering (only the fundamental is missing from the series).
Other instruments, like bells, chimes and tuned drums, make overtones that are not harmonics. For these in
Stop to think answers
- Vibrations B and C could have made by a string instrument (but not by a chime or a slide whistle), because the spectral content is (f, 2f, 3f, 4f…); Vibration A could be made by a slide whistle (but not a chime and probably not by a string). The spectral content contains only odd harmonics: (f, 3f, 5f, 7f…).
- Divide each of the overtone frequencies by the fundamental to get the spectral content: (520 Hz)/(200 Hz) = 2.76 and (1080 Hz)/(200 Hz) = 5.4. This is the same as for chimes.
- You can find the spectral content from the first note (see Stop to Think 2) and apply that to the 400 Hz note. An easier way is to recognize that the overtones of the 400 Hz bar will be double the overtones of the 200 Hz bar: 520 Hz * 2= 1140 Hz and 1080 Hz * 2 = 2160 Hz.
Image credits
- First five harmonics of C2 and their frequencies. Created by Abbott.
- FFTs of two vibrations with the same spectral content, but different fundamental frequency. Created by Abbott using desmos.com.
