3 Time graphs of common sounds

The vibrations that cause sound are (mostly) invisible- too small and too quick for the human eye to see. Sound engineers and scientists use graphs to make sense of vibrations and the sounds they cause. Time domain graphs are the most basic of these graphs.

Time domain graphs

A time domain graph shows how a quantity fluctuates over time. Time domain graphs are sometimes called history graphs. Time is plotted along the horizontal axis, so horizontal “distances” along the graph represent amounts of time. Almost any fluctuating quantity can be plotted on the vertical axis. The exact identity of the quantity on the vertical axis is often ignored- what’s fluctuating is usually less important than how that quantity is fluctuating.

To understand a time domain graph is, watch Spray Paint Oscillator (0:50 youTube video by the MIT Physics Demo Group) ^[1] now. The video shows a spray paint can bobbing up and down on the end of a spring as paper is pulled from right to left in front of spraying can. The paint trace on the paper is a record of where the spray can was (and when it was there). Time is recorded from left to right along the horizontal axis, while the location of the can is recorded along the vertical axis.

Simple harmonic motion

Most musical sounds are created by periodic vibrations- vibrations with a repeating pattern. The simplest of these is called simple harmonic oscillation (SHO for short).  The time domain graph of SHO is a sine curve. The MIT spray paint movie is an example of simple harmonic motion. Here is a time domain graph for SHO:

The sound caused by an SHO is often called pure tone, because the sound consists of a just a single frequency. The pure sine curve isn’t common in everyday sound, but it’s important because it’s the building block for all musical sounds.

Complex vibrations and overtones

When a musical instruments plays a note, the result is almost never a simple sine curve. Time domain graphs for these periodic vibrations have a regular, repeating pattern, but each cycle has a complicated shape. For lack of a better name, I will call these complex vibrations. Sounds made by most musical everyday instruments are complex vibrations.

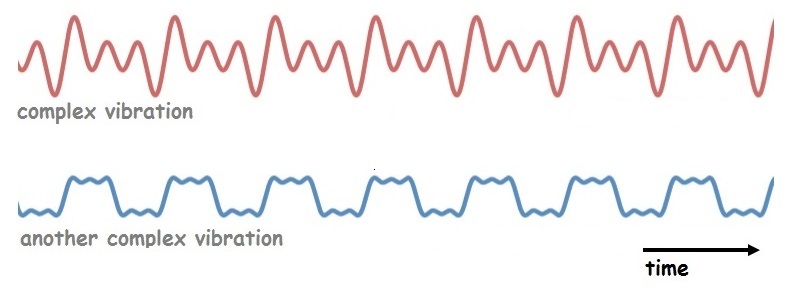
Complex vibrations are made up of many different SHO’s happening at the same time. Most musicians know this instinctively. When you play a note on an clarinet, you don’t hear just a single pure tone. Listen carefully and you hear that the single musical note is actually made up of many different pure tones, all going on at the same time.

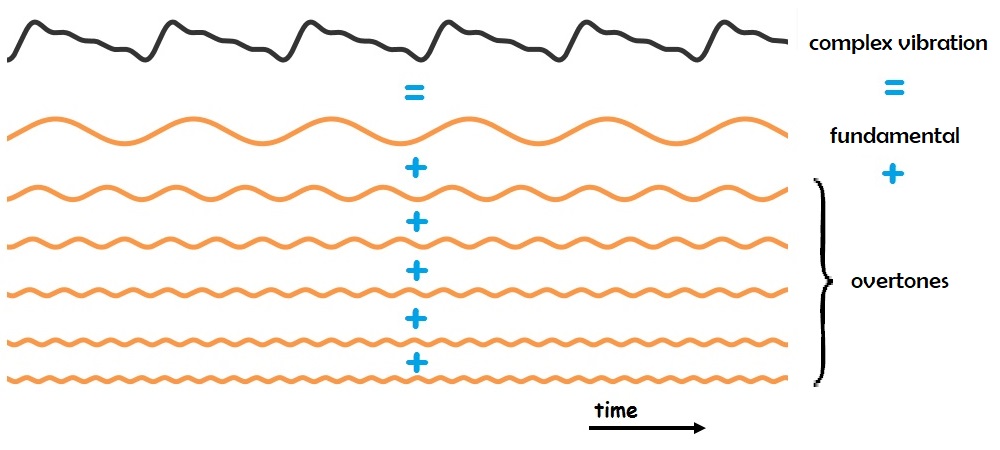
Complex vibrations are made up of many sine waves added together. The sine wave with the lowest frequency (longest period) in  complex vibration is called the fundamental. The other (higher frequency) components are called overtones. The fundamental is what our brains use to create the sensation of musical pitch. Overtones contribute to our perception of timbre- more on that in the section on perception.

The powerful idea that any complex vibration can be viewed as a sum of many sine waves is attributed to mathematician Joseph Fourier. Fourier invented mathematical techniques that provide a list of a sound’s “ingredients”- a list of which frequencies are present and in what amounts- from the time domain graph. Most audio software now includes Fourier analysis routines. Fourier’s ideas can also be used to build custom sounds-  that’s the idea behind most synthesizers.

Noise

Some vibrations don’t have a repeating pattern. These non-repeating vibrations are called aperiodic or noise. Sounds like “shhhh” are created by aperiodic vibrations. The time domain graphs of noise look chaotic- there’s no pattern.

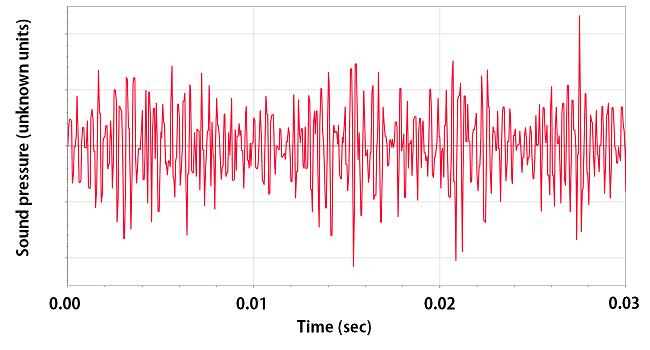
Because noise is aperiodic, the concepts of period and frequency don’t apply. Noise is made of a random mix of all possible frequencies.

Online resources

Watch Spray Paint Oscillator (0:50 youTube video) ^[2] to learn how to interpret time domain graphs.

Watch Coupled Oscillator ^[3] (0:26 youTube video) to see how it’s possible for a system to have two frequencies at the same time.

Image credits

1. Time domain graph of SHO: David Abbott; created using Desmos.com.
2. Time domain graph of two complex vibrations: David Abbott; created using Desmos.com.
3. Complex vibrations as the sum of sine curves: David Abbott; created using Desmos.com.
4. Time-domain graph of an aperiodic vibration (aka noise): David Abbott; created by saying “shhh” into a microphone using LoggerPro software.